题目内容

11．已知P为矩形ABCD所在平面内一点，AB=4，AD=3，$PA=\sqrt{5}$，$PC=2\sqrt{5}$，则$\overrightarrow{PB}•\overrightarrow{PD}$=（　　）
A．-5B．-5或0C．0D．5

分析 根据矩形的性质和勾股定理可判断$\overrightarrow{PB}$⊥$\overrightarrow{PD}$，继而可得$\overrightarrow{PB}$⊥$\overrightarrow{PD}$，问题得以解决．

解答 解：P为矩形ABCD所在平面内一点，AB=4，AD=3，
∴AC=5，
∵$PA=\sqrt{5}$，$PC=2\sqrt{5}$，
∴PA2+PC2=AC2，
∴PA⊥$\overrightarrow{PC}$，
∴$\overrightarrow{PB}$⊥$\overrightarrow{PD}$，
∴$\overrightarrow{PB}•\overrightarrow{PD}$=0，
故选：C．

点评 本题考查了向量的垂直和勾股定理，以及矩形的性质，属于基础题．

练习册系列答案
相关题目
1．已知集合M={-1，0，1}，N={y|y=1-cos$\frac{π}{2}$x，x∈M}，则集合M∩N的真子集的个数是（　　）
A．1B．2C．3D．4
2．平面向量$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{2π}{3}$，$\overrightarrow a=（2，0）$，$|\overrightarrow b|=1$，则$|\overrightarrow a+2\overrightarrow b|$=（　　）
A．1B．2C．$2\sqrt{3}$D．4
19．定义min{a，b}=$\left\{\begin{array}{l}{a，a≤b}\\{b，a＞b}\end{array}\right.$，已知实数x，y满足|x|≤2，|y|≤2，设z=min{x+y，2x-y}，则z的取值范围为[-6，3]．
6．已知θ是第四象限，且$sin（θ+\frac{π}{4}）=\frac{5}{13}$，则$tan（θ-\frac{π}{4}）$=-$\frac{12}{5}$．
16．在区间[0，1]上任选两个数x和y，则$y≥\sqrt{1-{x^2}}$的概率为（　　）
A．$\frac{π}{6}$B．$\frac{π}{4}$C．$1-\frac{π}{6}$D．$1-\frac{π}{4}$
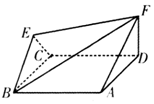3．如图，菱形ABCD与正三角形BCE的边长均为2，且平面ABCD⊥平面BCE，FD⊥平面ABCD，$FD=\sqrt{3}$．
（I）求证：EF∥平面ABCD；
（II）求证：平面ACF⊥平面BDF．
20．（x-$\frac{1}{\sqrt{x}}$）n的展开式中，所有二项式系数之和为512，则展开式中x3的系数为126（用数字作答）．
2．已知角α的终边经过点（3a-9，a+2），且sin2α≤0，sinα＞0，则a的取值范围是（　　）
A．（-2，3）B．[-2，3）C．（-2，3]D．[-2，3]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网