题目内容
抛物线y2=2px(p>0),其准线方程为x=-1,过准线与x轴的交点M做直线l交抛物线于A、B两点.
(Ⅰ)若点A为MB中点,求直线l的方程;
(Ⅱ)设抛物线的焦点为F,当AF⊥BF时,求△ABF的面积.
(Ⅰ)若点A为MB中点,求直线l的方程;
(Ⅱ)设抛物线的焦点为F,当AF⊥BF时,求△ABF的面积.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)通过抛物线方程求出p,设出直线的方程,与抛物线联立方程组,通过韦达定理结合点A为MB中点,即可求解直线l的方程;
(Ⅱ)利用AF⊥BF,结合向量的数量积,表示出三角形的面积,利用第一问韦达定理,即可求△ABF的面积.
(Ⅱ)利用AF⊥BF,结合向量的数量积,表示出三角形的面积,利用第一问韦达定理,即可求△ABF的面积.
解答:
(本小题满分13分)
解:(Ⅰ)∵抛物线的准线方程为x=-1
∴
=1,p=2-----------------------(1分)
∴抛物线的方程为y2=4x-----------------------(2分)
显然,直线l与坐标轴不平行
∴设直线l的方程为x=my-1,A(
,y1)B(
,y2)-----------------------(3分)
联立直线与抛物线的方程
,得y2-4my+4=0-----------------------(4分)
△=16m2-16>0,解得m<-1或m>1-----------------------(5分)
∵点A为MB中点,∴y1=
,即y2=2y1
∴y1y2=2y12=4,解得y1=±
-----------------------(6分)
y1+y2=4m,∴4m=
+2
或4m=-
-2
∴m=±
-----------------------(7分)
直线方程为4x-3
y+4=0或4x+3
y+4=0.-----------------------(8分)
(Ⅱ)焦点F(1,0),
=(
-1,y1),
=(
-1,y2)
∵AF⊥BF
∴(y1+y2)2=32-----------------------(11分)
-----------------------(13分)
解:(Ⅰ)∵抛物线的准线方程为x=-1
∴
| p |
| 2 |
∴抛物线的方程为y2=4x-----------------------(2分)
显然,直线l与坐标轴不平行
∴设直线l的方程为x=my-1,A(
| ||
| 4 |
| ||
| 4 |
联立直线与抛物线的方程
|
△=16m2-16>0,解得m<-1或m>1-----------------------(5分)
∵点A为MB中点,∴y1=
| 0+y2 |
| 2 |
∴y1y2=2y12=4,解得y1=±
| 2 |
y1+y2=4m,∴4m=
| 2 |
| 2 |
| 2 |
| 2 |
∴m=±
| 3 |
| 4 |
| 2 |
直线方程为4x-3
| 2 |
| 2 |
(Ⅱ)焦点F(1,0),
| FA |
| ||
| 4 |
| FB |
| ||
| 4 |
∵AF⊥BF
|
∴(y1+y2)2=32-----------------------(11分)
|
点评:本题考查直线与圆锥曲线的位置关系及抛物线方程的求解,考查向量在几何正中定义域,考查学生分析问题解决问题的能力,解决本题的关键是韦达定理的应用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
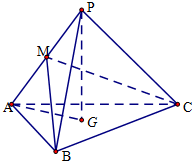 如图,三棱锥P-ABC中,AB=AC=2
如图,三棱锥P-ABC中,AB=AC=2