题目内容
已知回归直线通过样本点的中心,若x与y之间的一组数据:
则y与x的线性回归方程
=
x+
所表示的直线必过点( )
| x | 0 | 1 | 2 | 3 |
| y | 1.1 | 3.1 | 4.9 | 6.9 |
| ∧ |
| y |
| ∧ |
| b |
| ∧ |
| a |
A、(
| ||
| B、(1,2) | ||
| C、(2,2) | ||
D、(
|
考点:线性回归方程
专题:计算题,概率与统计
分析:求出x、y的平均值,回归直线方程一定过样本的中心点(
,
),代入可得答案.
. |
| x |
. |
| y |
解答:
解:回归直线方程一定过样本的中心点(
,
),
=
=
,
=
=4,
∴样本中心点是(
,4),
则y与x的线性回归方程y=bx+a必过点(
,4),
故选:A.
. |
| x |
. |
| y |
. |
| x |
| 0+1+2+3 |
| 4 |
| 3 |
| 2 |
. |
| y |
| 1.1+3.1+4.9+6.9 |
| 4 |
∴样本中心点是(
| 3 |
| 2 |
则y与x的线性回归方程y=bx+a必过点(
| 3 |
| 2 |
故选:A.
点评:本题考查平均值的计算方法,回归直线的性质:回归直线方程一定过样本的中心点(
,
).
. |
| x |
. |
| y |

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
下列函数中,是指数函数的是( )
| A、y=(-2)x | ||
B、y=(
| ||
| C、y=x2 | ||
| D、y=x-1 |
三棱柱ABC-A1B1C1中,AA1=2且AA1⊥平面ABC,△ABC是边长为
的正三角形,该三棱柱的六个顶点都在一个球面上,则这个球的体积为( )
| 3 |
| A、8π | ||||
B、
| ||||
C、
| ||||
D、8
|
已知双曲线C:
-
=1的焦距为10,点P(1,2)在C的渐近线上,则C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知某空间几何体的三视图如图所示,则( )
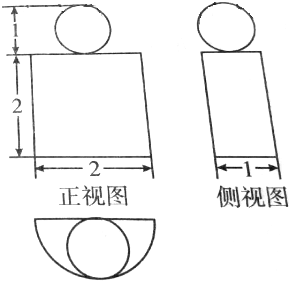

| A、该几何体的表面积为4+2π | ||
B、该几何体的体积为
| ||
| C、该几何体的表面积为4+4π | ||
| D、该几何体的体积为π |
设a,b,c依次是方程x+sinx=1,x+sinx=2,x+
sinx=2的根,并且0<x<
,则a,b,c的大小关系是( )
| 1 |
| 2 |
| π |
| 2 |
| A、a<b<c |
| B、a<c<b |
| C、c<b<a |
| D、b<c<a |
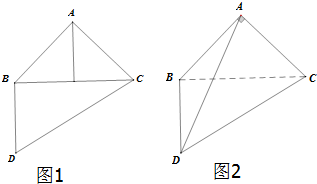 如图1,△ABC是等腰三角形,其中∠A=90°,且DB⊥BC,∠BCD=30°,现将△ABC沿边BC折起,使得二面角A-BC-D大小为30°(如图2),则异面直线BC与AD所成的角为( )
如图1,△ABC是等腰三角形,其中∠A=90°,且DB⊥BC,∠BCD=30°,现将△ABC沿边BC折起,使得二面角A-BC-D大小为30°(如图2),则异面直线BC与AD所成的角为( )