Question

【题目】研究下列函数的定义域、值域、奇偶性和单调性，并作出其大致图像．

（1）；

（2）；

（3）；

（4）．

Answer 1

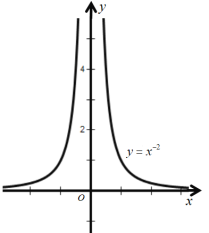
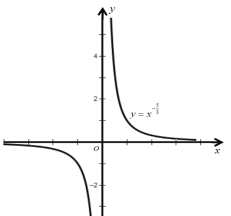
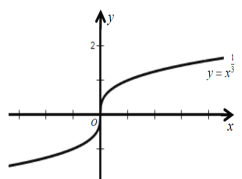
【答案】（1）定义域：；值域：；偶函数；在上单调递增，在上单调递减；图像见解析；（2）定义域：；值域：；奇函数：在和上单调递减；图像见解析；（3）定义域；R；值域：R；奇函数；在上单调递增；图像见解析；（4）定义域：值域：；非奇非偶函数；在上单调递增；图像见解析

【解析】

将幂函数化为根式的形式，分析其定义域和值域，由奇偶性的定义判断其奇偶性，由指数的正负结合幂函数的性质先判断出函数在第一象限内的单调性，再根据奇偶性得出单调区间，作出其大致图像.

（1），设，的定义域为，

因为，所以值域为：

显然，为偶函数，

在中，，为偶函数，所以在上单调递增，在上单调递减.

（2），设，定义域：，

由，所以值域：，

由，所以奇函数，

在中，，为奇函数，所以在上单调递减，在上单调递减.

（3），设，所以定义域；R；值域：R；

由，所以奇函数，

在中，，在上单调递增.

（4），设，由得定义域：值域：

因为定义域：，所以非奇非偶函数；

在中，，定义域为，所以在上单调递增；