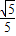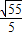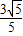Question

已知点A（1-t，1-t，t），B（2，t，t），则A、B两点距离的最小值为（　　）

• A．

  5

  5

• B．

  55

  5

• C．

  3 5

  5

• D．2

Answer 1

分析：由两点的距离公式，算出|AB|²关于t的式子，结合二次函数的性质可得t=

3

5

时，|AB|²有最小值，相应地A、B两点距离也取得最小值．

解答：解：∵点A（1-t，1-t，t），B（2，t，t），
∴|AB|²=（t-1）²+（2t-1）²+（t-t）²=5t²-6t+2
∵t=

3

5

时，|AB|²=5t²-6t+2取得最小值

1

5

∴当t=

3

5

时，|AB|的最小值为

5

5

解：A

点评：本题给出两点含有字母参数t的坐标，求两点间的最短距离，着重考查了两点间的距离公式和二次函数的性质等知识，属于基础题．