题目内容
12.甲、乙两位同学约定周日早上8:00-8:30在学校门口见面,已知他们到达学校的时间是随机的,则甲要等乙至少10分钟才能见面的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{9}$ |
分析 由题意知本题是一个几何概型,试验包含的所有事件是Ω={(x,y)|0≤x≤30,0≤y≤30},做出事件对应的集合表示的面积,写出满足条件的事件是A={(x,y)|0≤x≤30,0≤y≤30,y-x≥10},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
解答  解:由题意知本题是一个几何概型,
解:由题意知本题是一个几何概型,
试验包含的所有事件是Ω={(x,y)|0≤x≤30,0≤y≤30}
事件对应的集合表示的面积是s=900,
满足条件的事件是A={(x,y)|0≤x≤30,0≤y≤30,y-x≥10},事件对应的集合表示的面积是$\frac{1}{2}×20×20$=200,
根据几何概型概率公式得到P=$\frac{2}{9}$.
故选C.
点评 本题是一个几何概型,对于这样的问题,一般要通过把试验发生包含的事件所对应的区域求出,根据集合对应的图形面积,用面积的比值得到结果.

练习册系列答案
相关题目
7.设m,n为两条不同的直线,α为平面,则下列结论正确的是( )
| A. | m⊥n,m∥α⇒n⊥α | B. | m⊥n,m⊥α⇒n∥α | C. | m∥n,m∥α⇒n∥α | D. | m∥n,m⊥α⇒n⊥α |
4. 某几何体的正视图和侧视图如图①,它的俯视图的直观图为矩形O1A1B1C1如图②,其中O1A1=6,O1C1=2,则该几何体的体积为( )
某几何体的正视图和侧视图如图①,它的俯视图的直观图为矩形O1A1B1C1如图②,其中O1A1=6,O1C1=2,则该几何体的体积为( )
 某几何体的正视图和侧视图如图①,它的俯视图的直观图为矩形O1A1B1C1如图②,其中O1A1=6,O1C1=2,则该几何体的体积为( )
某几何体的正视图和侧视图如图①,它的俯视图的直观图为矩形O1A1B1C1如图②,其中O1A1=6,O1C1=2,则该几何体的体积为( )| A. | 16$\sqrt{2}$ | B. | 32$\sqrt{2}$ | C. | 32 | D. | 64 |
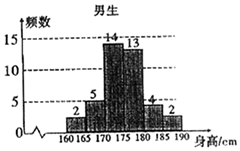 为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样检查,测得身高情况的统计图如下:
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样检查,测得身高情况的统计图如下: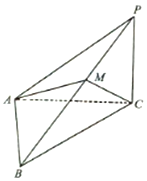 如图,在三棱锥P-ABC中,PC⊥平面ABC,∠ACB=45°,BC=2$\sqrt{2}$,AB=2.
如图,在三棱锥P-ABC中,PC⊥平面ABC,∠ACB=45°,BC=2$\sqrt{2}$,AB=2.