题目内容
18.某三棱锥的三视图如图所示,其中左视图中虚线平分底边,则该三棱锥的所有面中最大面的面积是( )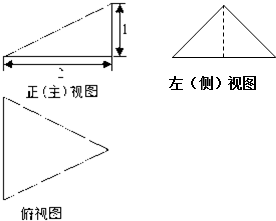
| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
分析 根据几何体的三视图,得出该几何体是侧棱垂直于底面的三棱锥,根据题意画出图形,结合图形求出它的各个面面积,可得答案.
解答 解:根据几何体的三视图,得几何体的直观图为:
该几何体是如图所示的三棱锥,且侧棱PC⊥底面ABC;
所以,S△ABC=$\frac{1}{2}$×2×2=2,
S△PAC=S△PBC=$\frac{1}{2}$×$\sqrt{{2}^{2}+{1}^{2}}$×1=$\frac{\sqrt{5}}{2}$,
S△PAB=$\frac{1}{2}$×2×$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$;
故选:B.
点评 本题考查了空间几何体三视图的应用问题,解题时应根据三视图画出几何图形,求出各个面的面积,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知函数f(x)=x2-2ax+5(a>1),g(x)=log3x,若函数f(x)的定义域与值域都是[1,a],则对于任意的x1,x2∈[1,a+1]时,总有$|{f({x_1})-g({x_2})}|≤{t^2}+2t-1$恒成立,则t的取值范围为( )
| A. | [1,3] | B. | [-1,3] | C. | [1,+∞)∪(-∞,-3] | D. | [3,+∞)∪(-∞,-1] |
 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别 是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别 是PC,PD,BC的中点.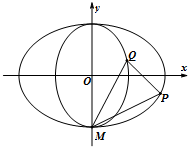 如图,中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$.
如图,中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$.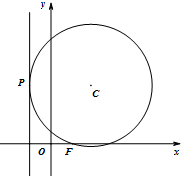 如图,动圆C过点F(1,0),且与直线x=-1相切于点P.
如图,动圆C过点F(1,0),且与直线x=-1相切于点P.