题目内容
17．在${（{4{x^2}-\frac{1}{x}}）^6}$的展开式中，x-3的系数为-24．（用数字作答）分析 在二项展开式的通项公式中，令x的幂指数等于-3，求出r的值，即可求得x-3的系数．
解答 解：${（{4{x^2}-\frac{1}{x}}）^6}$的展开式的通项公式为Tr+1=${C}_{6}^{r}$•（4x2）6-r•（-$\frac{1}{x}$）r=（-1）r•46-r•${C}_{6}^{r}$•x12-3r，
令12-3r=-3，解得r=5，∴展开式中x-3的系数为-24．
故答案为-24．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于中档题．
练习册系列答案
相关题目
8．已知偶函数f（x）在[0，+∞）上是增函数，且f（1）=0，则满足f（log${\;}_{\frac{1}{2}}$x）＞0的x的取值范围是（ ）
| A． | （0，+∞） | B． | （0，$\frac{1}{2}$）∪（2，+∞） | C． | （0，$\frac{1}{2}$） | D． | （0，$\frac{1}{2}$）∪（1，2） |
12．已知△ABC是钝角三角形，若AC=1，BC=2，且△ABC的面积为$\frac{{\sqrt{3}}}{2}$，则AB=（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{7}$ | C． | $2\sqrt{2}$ | D． | 3 |
9．从数字1，2，3，4，5，6中任取两个数，则取出的两个数的乘积为奇数的概率为（ ）
| A． | $\frac{1}{15}$ | B． | $\frac{2}{15}$ | C． | $\frac{1}{5}$ | D． | $\frac{4}{15}$ |
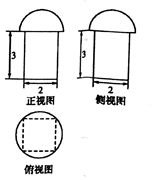
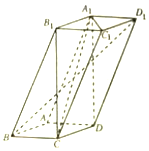如图，四棱柱ABCD-A1B1C1D1中，A1D⊥平面ABCD，底面为边长为1的正方形，侧棱AA1=2