题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{{2}^{x},x≤0}\end{array}\right.$,则f($\frac{1}{4}$)+f(-2)的值为-$\frac{7}{4}$.分析 利用分段函数的性质即可得出.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{{2}^{x},x≤0}\end{array}\right.$,
∴f($\frac{1}{4}$)=$lo{g}_{2}\frac{1}{4}$=-2.
f(-2)=2-2=$\frac{1}{4}$.
则f($\frac{1}{4}$)+f(-2)=-2+$\frac{1}{4}$=-$\frac{7}{4}$.
故答案为:$-\frac{7}{4}$.
点评 本题考查了分段函数的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.已知函数f(x)=10x-|lg(-x)|有两个零点x1,x2,则( )
| A. | $\frac{1}{10}$<x1x2<1 | B. | $\frac{1}{2}$<x1x2<1 | C. | $\frac{1}{e}$<x1x2<1 | D. | 1<x1x2<e |
 ,且
,且 在
在 上单调递减,则
上单调递减,则 ___________.
___________.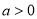 ,设命题
,设命题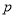 :函数
:函数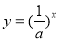 为增函数;命题
为增函数;命题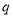 :当
:当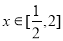 时,
时,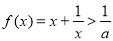 恒成立.如果
恒成立.如果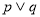 为真命题,
为真命题,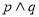 为假命题,求
为假命题,求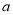 的范围.
的范围.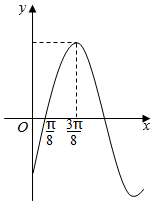 函数f(x)=Asin(ωx-$\frac{π}{4}$)(A>0,ω>0)的部分图象如图所示.
函数f(x)=Asin(ωx-$\frac{π}{4}$)(A>0,ω>0)的部分图象如图所示.