题目内容
1.已知函数f(x)=10x-|lg(-x)|有两个零点x1,x2,则( )| A. | $\frac{1}{10}$<x1x2<1 | B. | $\frac{1}{2}$<x1x2<1 | C. | $\frac{1}{e}$<x1x2<1 | D. | 1<x1x2<e |
分析 作出y1=10x,y2=|lg(-x)|的图象,得出两函数图象有两个交点,设横坐标为x1,x2且|lg(-x1)|<|lg(-x2)|,得出0<x1x2<1,再结合零点存在定理,可得$\frac{1}{e}$<x1x2<1.
解答 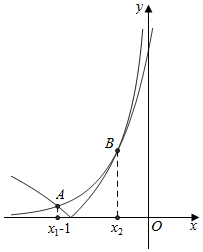 解:设y1=10x,y2=|lg(-x)|,画出两函数的图象,如右图,
解:设y1=10x,y2=|lg(-x)|,画出两函数的图象,如右图,
其中,红色曲线为y1的图象,紫色曲线为y2的图象,
设两图象的交点为A,B,其横坐标为x1,x2,
不妨设x1<-1<x2,由图可知,|lg(-x1)|<|lg(-x2)|,
所以,lg(-x1)<-lg(-x2),因此,lg(x1x2)<0,
解得,0<x1x2<1,----------------------------①
又因为f(-1)=$\frac{1}{10}$>0,f(-$\frac{1}{e}$)=$\frac{1}{1{0}^{\frac{1}{e}}}$-lge<0,
所以,-1<x2<-$\frac{1}{e}$,而x1<-1,
所以,x1x2>$\frac{1}{e}$,-------------------------------②
综合①②得,$\frac{1}{e}$<x1x2<1,
故答案为:C.
点评 本题主要考查了函数的零点与方程根的关系,以及数形结合的数学思想和分析解决问题的能力,正确作出函数图象是关键,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
10.直线$\sqrt{3}$x+y=0的倾斜角为( )
| A. | 30° | B. | 90° | C. | 120° | D. | 150° |
 在点
在点 处的切线与
处的切线与 平行,则
平行,则 ( )
( ) 在
在 上是增函数,则实数
上是增函数,则实数 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
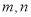 ,定义某种运算“※”,法则如下:当
,定义某种运算“※”,法则如下:当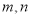 都是正奇数时,
都是正奇数时,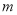 ※
※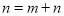 ;当
;当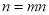 ,则在此定义下,集合
,则在此定义下,集合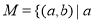 ※
※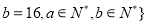 的真子集的个数是( )
的真子集的个数是( )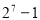 B.
B.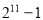 C.
C.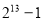 D.
D.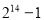
 ,在区间
,在区间 上单调递减,则实数
上单调递减,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.