题目内容
8.已知函数f(x)=sin(πx-$\frac{π}{3}$),若函数y=f(asinx+1),x∈R没有零点,则实数a的取值范围是(-$\frac{1}{3}$,$\frac{1}{3}$).分析 由f(x)没有零点求得x的范围,再根据f(asinx+1)没有零点可得asinx+1的范围,根据正弦函数的值域,分类讨论求得a的范围.
解答 解:若函数f(x)=sin(πx-$\frac{π}{3}$)=sinπ(x-$\frac{1}{3}$)没有零点,
故0<(x-$\frac{1}{3}$)π<π,或-π<(x-$\frac{1}{3}$)π<0,
即 0<(x-$\frac{1}{3}$)<1,或-1<(x-$\frac{1}{3}$)<0,
即$\frac{1}{3}$<x<$\frac{4}{3}$ 或-$\frac{2}{3}$<x<$\frac{1}{3}$.
由于函数y=f(asinx+1),x∈R没有零点,则$\frac{1}{3}$<asinx+1<$\frac{4}{3}$,或-$\frac{2}{3}$<asinx+1<$\frac{1}{3}$,
当a>0时,∵1-a≤asinx+1≤1+a,$\left\{\begin{array}{l}{1-a>\frac{1}{3}}\\{1+a<\frac{4}{3}}\end{array}\right.$ 或$\left\{\begin{array}{l}{1-a>-\frac{2}{3}}\\{1+a<\frac{1}{3}}\end{array}\right.$,
解得0<a<$\frac{1}{3}$.
当a<0时,1+a≤asinx+1≤1-a,∴$\left\{\begin{array}{l}{1+a>\frac{1}{3}}\\{1-a<\frac{4}{3}}\end{array}\right.$或 $\left\{\begin{array}{l}{1+a>-\frac{2}{3}}\\{1-a<\frac{1}{3}}\end{array}\right.$,
求得-$\frac{1}{3}$<a<0.
当a=0时,函数y=f(asinx+1)=f(1)=sin$\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$≠0,满足条件.
综上可得,a的范围为(-$\frac{1}{3}$,$\frac{1}{3}$).
故答案为:(-$\frac{1}{3}$,$\frac{1}{3}$).
点评 本题主要考查正弦函数的图象特征,函数的零点的定义,属于中档题.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案| A. | 第一或第二象限的角 | B. | 第二或第四象限的角 | ||
| C. | 第一或第三象限的角 | D. | 第二或第三象限的角 |
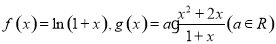 .
.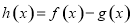 在定义域内单调递减,求
在定义域内单调递减,求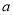 的取值范围;
的取值范围;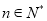 ,证明:
,证明: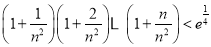 (
(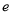 为自然对数的底数).
为自然对数的底数).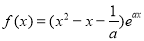 (
(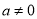 ).
).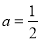 时,求函数
时,求函数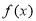 的零点;
的零点;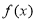 的单调区间;
的单调区间;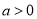 时,若
时,若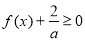 对
对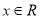 恒成立,求
恒成立,求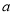 的取值范围.
的取值范围. ,在区间
,在区间 上单调递减,则实数
上单调递减,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.