题目内容
10.已知函数f(x)=ex-kx,x∈R,k为常数,e是自然对数的底数.(Ⅰ)当k=e时,证明f(x)≥0恒成立;
(Ⅱ)若k>0,且对于任意x≥0,f(x)>0恒成立,试确定实数k的取值范围.
分析 (Ⅰ)当k=e时,求出函数的f'(x)=ex-e,利用导函数的符号判断单调性,求出函数的最小值,推出结果.
(Ⅱ)解法一:当x=0时原不等式恒成立,所以k∈R,当x>0时,不等式化简为时,不等式化简为$k<\frac{e^x}{x}$,$令g(x)=\frac{e^x}{x},则g'(x)=\frac{{{e^x}(x-1)}}{x^2}$,利用单调性求解函数的最值,推出结果.
解法二:f'(x)=ex-k=0可得x=lnk.通过①当k∈(0,1]时,②当k∈(1,+∞)时,分别求解函数的单调区间函数的最值,图象结果即可.
解答 (本题满分12分)
(Ⅰ)证明:当k=e时,f(x)=ex-ex,∴f'(x)=ex-e
由f'(x)>0得x>1,故f(x)的单调递增区间为(1,+∞);f'(x)<0得x<1,故f(x)的单调递减区间为(-∞,1);
所以函数有最小值为f(1)=e-e=0,所以f(x)≥0恒成立. …(5分)
(Ⅱ)解法一:当x=0时原不等式恒成立,所以k∈R…(6分)
当x>0时,不等式化简为时,不等式化简为$k<\frac{e^x}{x}$$令g(x)=\frac{e^x}{x},则g'(x)=\frac{{{e^x}(x-1)}}{x^2}$;∴g(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
因为g(x)min=g(1)=e,所以k<e;…(11分)
又k>0,所以0<k<e.…(12分)
解法二:f'(x)=ex-k=0可得x=lnk.
①当k∈(0,1]时,f'(x)=ex-k>1-k≥0(x>0).
此时f(x)在区间[0,+∞)上单调递增.故f(x)≥f(0)=1>0,符合题意.…(8分)
②当k∈(1,+∞)时,lnk>0.当x变化时f'(x),f(x)的变化情况如下表:
| x | (0,lnk) | lnk | (lnk,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
依题意k-klnk>0又k>1所以1<k<e. …(11分)
由①②得,实数k的取值范围是0<k<e.…(12分)
点评 本题考查函数的导数的应用,函数的单调性以及函数的最值的求法,考查转化思想以及计算能力,分类讨论思想的应用.

| A. | $(-∞,\sqrt{3}-1]$ | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | $(-∞,1-\sqrt{3}]$ |
命题p::若在边长为1的正方形ABCD内任取一点M,则|MA|≤1的概率为$\frac{π}{4}$.
命题q:若从一只只有3枚一元硬币和2枚五角硬币的储钱罐内随机取出2枚硬币(假设每枚硬币被抽到都是等可能的),则总共取到2圆钱的概率为$\frac{1}{3}$.那么,下列命题中为真命题的是( )
| A. | p∧q | B. | ?p | C. | p∧(?q) | D. | (?p)∧(?q) |
| A. | $\overrightarrow{AB}=\overrightarrow{OC}$ | B. | $\overrightarrow{AB}∥\overrightarrow{DE}$ | C. | $|{\overrightarrow{AD}}|=|{\overrightarrow{BE}}|$ | D. | $|{\overrightarrow{AC}}|=|{\overrightarrow{BE}}|$ |
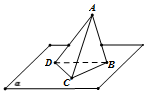 如图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=4,AD=2$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是 $2\sqrt{3}π$.
如图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=4,AD=2$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是 $2\sqrt{3}π$.