题目内容
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与函数y=$\sqrt{x}$(x≥0)的图象交于点P,若函数y=$\sqrt{x}$的图象与点P处的切线过双曲线左焦点F(-4,0),则双曲线的离心率是( )| A. | $\frac{\sqrt{17}+4}{4}$ | B. | $\frac{\sqrt{17}+3}{4}$ | C. | $\frac{\sqrt{17}+2}{4}$ | D. | $\frac{\sqrt{17}+1}{4}$ |
分析 设P的坐标为(m,$\sqrt{m}$),求函数导数,利用导数的几何意义以及切线斜率公式建立方程关系求出m=4,根据双曲线的定义求出a,c即可.
解答 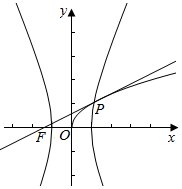 解:设P的坐标为(m,$\sqrt{m}$),左焦点F(-4,0),
解:设P的坐标为(m,$\sqrt{m}$),左焦点F(-4,0),
函数的导数f′(x)=$\frac{1}{2\sqrt{x}}$,则在P处的切线斜率k=f′(m)=$\frac{1}{2\sqrt{m}}$=$\frac{\sqrt{m}}{m+4}$,
即m+4=2m,得m=4,
则P(4,2),设右焦点为A(4,0),
则2a=|PF|-|PA|=$\sqrt{64+4}-\sqrt{0+4}$=2($\sqrt{17}-1$),
即a=$\sqrt{17}-1$,
∵c=4,
∴双曲线的离心率e=$\frac{c}{a}$=$\frac{\sqrt{17}+1}{4}$,
故选:D
点评 本题考查双曲线的离心率的求法,根据导数的几何意义,建立切线斜率关系,求出a,c是解决本题的关键.考查运算能力.

练习册系列答案
相关题目
9.已知点P在双曲线$\frac{x^2}{a^2}-\frac{y^2}{16}$=1的右支上,F为双曲线的左焦点,Q为线段PF的中点,O为坐标原点.若|OQ|的最小值为1,则双曲线的离心率为( )
| A. | $\frac{17}{15}$ | B. | $\frac{15}{17}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
7.设a,b是不相等的两个正数,且blna-alnb=a-b,给出下列结论:①a+b-ab>1;②a+b>2;③$\frac{1}{a}$+$\frac{1}{b}$>2.其中所有正确结论的序号是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
8.过抛物线y2=2px(p>0)的焦点F,且倾斜角为$\frac{π}{4}$的直线与抛物线交于A,B两点,若AB的垂直平分线经过点(0,2),M为抛物线上的一个动点,则M到直线11:5x-4y+4=0和l2:x=-$\frac{2}{5}$的距离之和的最小值为( )
| A. | $\frac{6\sqrt{41}}{41}$ | B. | $\frac{6\sqrt{31}}{31}$ | C. | $\frac{3\sqrt{41}}{41}$ | D. | $\frac{3\sqrt{31}}{31}$ |
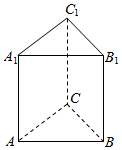 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=AC=2,AA1=4
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=AC=2,AA1=4