题目内容
设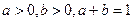 求证:
求证: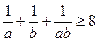 (用两种方法证明).
(用两种方法证明).
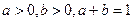 求证:
求证: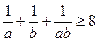 (用两种方法证明).
(用两种方法证明).证明略
证明:方法一:综合法
 ,
,

 ,
, (当且仅当
(当且仅当 时取等号),
时取等号),
又 (当且仅当
(当且仅当 时取等号),
时取等号),
 (当且仅当
(当且仅当 时取等号).
时取等号).
方法二:分析法
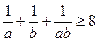









 ,
,
由基本不等式可知,当 时,
时, 成立,(当且仅当
成立,(当且仅当 时取等号),所以原不等式成立.
时取等号),所以原不等式成立.
 ,
, 
 ,
, (当且仅当
(当且仅当 时取等号),
时取等号),又
 (当且仅当
(当且仅当 时取等号),
时取等号), (当且仅当
(当且仅当 时取等号).
时取等号).方法二:分析法
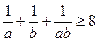









 ,
,由基本不等式可知,当
 时,
时, 成立,(当且仅当
成立,(当且仅当 时取等号),所以原不等式成立.
时取等号),所以原不等式成立.
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
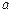 与
与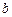 不共面,直线
不共面,直线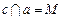 ,直线
,直线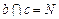 ,又
,又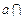 平面
平面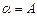 ,
,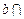 平面
平面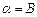 ,
,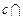 平面
平面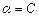 ,求证:
,求证: 三点不共线.
三点不共线.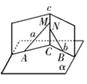
 中,若
中,若 ,则
,则 ,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想
,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想 ,求证
,求证


 为虚数单位
为虚数单位 ,若
,若 为纯虚数,则
为纯虚数,则 = .
= . …
… >
> (n∈N*,且n>2)时,第二步由
(n∈N*,且n>2)时,第二步由
 +
+ -
- 
 +
+