题目内容
8.已知α、β是两个平面,m,n是α、β外的两条直线,给出四个论断:①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中三个为条件,余下的一个为结论,能组成正确命题的个数为2.分析 构造长方体ABCD-A1B1C1D1,然后以四个论断中的其中三个为条件,推导第4个,借助于长方体中的线与面进行合理构造,然后进行合理推理,得出正确结论.
解答 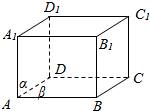 解:如图,做出长方体ABCD-A1B1C1D1,下面判断一下四个命题:
解:如图,做出长方体ABCD-A1B1C1D1,下面判断一下四个命题:
(1)①m⊥n;②α⊥β;③n⊥β⇒④m⊥α.在长方体ABCD-A1B1C1D1中,令面ADD1A1为α,面ABCD为β,直线CC1为n,A1C1为m,显然m不与α垂直,所以此命题是假命题;
(2)①m⊥n;②α⊥β;④m⊥α⇒③n⊥β.此命题和上一命题是一样的,所以也是假命题;
(3)①m⊥n;③n⊥β;④m⊥α⇒②α⊥β.由已知,$\overrightarrow{m}$、$\overrightarrow{n}$分别是面α,β的法向量,因为m⊥n,所以$\overrightarrow{m}$⊥$\overrightarrow{n}$,所以α⊥β,所以此命题是真命题;也可以利用长方体进行直观判断;
(4)②α⊥β;③n⊥β;④m⊥α⇒①m⊥n.在长方体ABCD-A1B1C1D1中,令面ADD1A1为α,面ABCD为β,直线D1C1为m,CC1为n,则m⊥n.所以此命题为真命题.
故正确命题有两个.
故答案为:2.
点评 长方体是判断有关空间线、面之间垂直关系的重要载体,特别是在选择题中,主要是根据已知与结论,合理选择线与面,然后做出正确的判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知命题p:?x0∈(-∞,0),2${\;}^{{x}_{0}}$<1,命题q:?x∈R,x+$\frac{1}{x}$≥2,则( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
20.设集合A={0,1,2,4},B={x∈R|1<x≤4},则A∩B=( )
| A. | {1,2,3,4} | B. | {2,3,4} | C. | {2,4} | D. | {x|1<x≤4} |