题目内容
(本小题满分14分)
已知数列 满足
满足
 ,
, (
( ,
, ),
),
若数列 是等比数列.
是等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求证:当 为奇数时,
为奇数时, ;
;
(Ⅲ)求证: (
( ).
).
已知数列
 满足
满足
 ,
, (
( ,
, ),
),若数列
 是等比数列.
是等比数列.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)求证:当
 为奇数时,
为奇数时, ;
;(Ⅲ)求证:
 (
( ).
).略
(Ⅰ)∵数列 是等比数列
是等比数列
∴ 应为常数
应为常数
∴ 得
得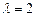 或
或 当
当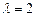 时,可得
时,可得 为首项是
为首项是 ,
,
公比为 的等比数列,则
的等比数列,则 ①
①
当 时,
时, 为首项是
为首项是 ,公比为
,公比为 的等比数列,
的等比数列,
∴ ② ①-②得,
② ①-②得,  ………4分
………4分
(注:也可由①利用待定系数或同除 得通项公式)
得通项公式)
(Ⅱ)当 为奇数时,
为奇数时,
 ∴
∴  ………8分
………8分
(Ⅲ)由(Ⅱ)知 为奇数时,
为奇数时,  ………10分
………10分
①当 为偶数时,
为偶数时, 
②当 为奇数时,
为奇数时,

 ………13分
………13分
 是等比数列
是等比数列∴
 应为常数
应为常数∴
 得
得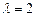 或
或 当
当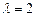 时,可得
时,可得 为首项是
为首项是 ,
,公比为
 的等比数列,则
的等比数列,则 ①
①当
 时,
时, 为首项是
为首项是 ,公比为
,公比为 的等比数列,
的等比数列,∴
 ② ①-②得,
② ①-②得,  ………4分
………4分(注:也可由①利用待定系数或同除
 得通项公式)
得通项公式)(Ⅱ)当
 为奇数时,
为奇数时,
 ∴
∴  ………8分
………8分(Ⅲ)由(Ⅱ)知
 为奇数时,
为奇数时,  ………10分
………10分①当
 为偶数时,
为偶数时, 
②当
 为奇数时,
为奇数时,

 ………13分
………13分
练习册系列答案
相关题目
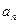 },{
},{ },{
},{ }满足a0=1,b0=1,c0=0,且
}满足a0=1,b0=1,c0=0,且 +2,
+2, ,
, +
+ 所表示的平面区域为D
所表示的平面区域为D ,记D
,记D (整点即横坐标和纵坐标均为整数的点).
(整点即横坐标和纵坐标均为整数的点).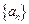 的通项
的通项 公式
公式 ;
; ,记
,记 ,求证:
,求证: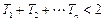 .
. 为数列
为数列 的前n项和,且对任意
的前n项和,且对任意 都有
都有 ,记
,记
 ;
; 与
与 的大小;
的大小; 。
。 成立;
成立; -1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
-1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。 ”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作
”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作 ,
, ,其中
,其中 为数列
为数列 中的第
中的第 项.若
项.若 ________.
________.  满足
满足 ,若
,若 ,则
,则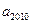 的值为________.
的值为________. 中,
中, 是前
是前 项和,
项和, ,
, ,则
,则 的值为_ ___
的值为_ ___  是等差数列
是等差数列 的前n项和,且
的前n项和,且 的值为
的值为