题目内容
(本小题共14分)已知函数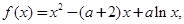 其中常数
其中常数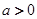 .
.
(1)当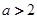 时,求函数
时,求函数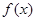 的单调递增区间;
的单调递增区间;
(2)当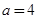 时,若函数
时,若函数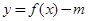 有三个不同的零点,求m的取值范围;
有三个不同的零点,求m的取值范围;
(3)设定义在D上的函数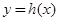 在点
在点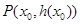 处的切线方程为
处的切线方程为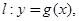 当
当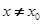 时,若
时,若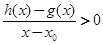 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数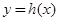 的“类对称点”,请你探究当
的“类对称点”,请你探究当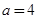 时,函数
时,函数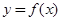 是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
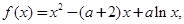 其中常数
其中常数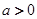 .
.(1)当
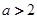 时,求函数
时,求函数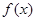 的单调递增区间;
的单调递增区间;(2)当
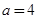 时,若函数
时,若函数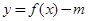 有三个不同的零点,求m的取值范围;
有三个不同的零点,求m的取值范围;(3)设定义在D上的函数
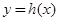 在点
在点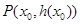 处的切线方程为
处的切线方程为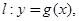 当
当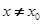 时,若
时,若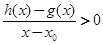 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数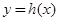 的“类对称点”,请你探究当
的“类对称点”,请你探究当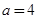 时,函数
时,函数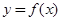 是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.(1)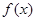 的单调递增区间为
的单调递增区间为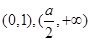 .(2)
.(2)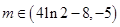 .
.
(3)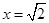 是一个类对称点的横坐标.
是一个类对称点的横坐标.
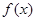 的单调递增区间为
的单调递增区间为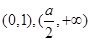 .(2)
.(2)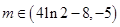 .
.(3)
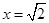 是一个类对称点的横坐标.
是一个类对称点的横坐标.试题分析:(1)由f′(x)="2x-(a+2)+"
 =
=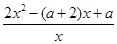 =
=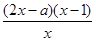
,能求出当a>2时,求函数f(x)的单调递增区间.
(2)a=4,f′(x)=2x+
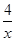 -6,故f′(x)="2x+"
-6,故f′(x)="2x+" 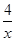 -6≥4
-6≥4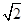 -6,不存在6x+y+m=0这类直线的切线.
-6,不存在6x+y+m=0这类直线的切线.(3)y=g(x)=(2x0+
 -6)(x-x0)+
-6)(x-x0)+ 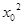 -6x0+4lnx0,令h(x)=f(x)-g(x),由此入手,能够求出一个“类对称点”的横坐标.
-6x0+4lnx0,令h(x)=f(x)-g(x),由此入手,能够求出一个“类对称点”的横坐标.解:(1)由
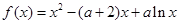 可知,函数的定义域为
可知,函数的定义域为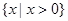 ,
,且
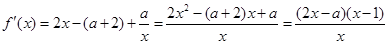 .
.因为
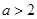 ,所以
,所以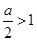 .
.当
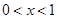 或
或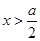 时,
时,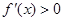 ;当
;当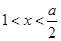 时,
时,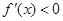 ,
,所以
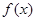 的单调递增区间为
的单调递增区间为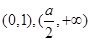 .
.(2)当
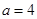 时,
时,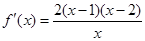 .
.所以,当
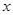 变化时,
变化时,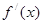 ,
,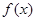 的变化情况如下:
的变化情况如下: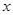 | (0,1) | 1 | (1,2) | 2 | (2,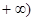 |
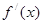 | + | 0 | — | 0 | + |
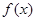 | 单调递增 | 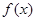 取极大值 取极大值 | 单调递减 | 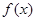 取极小值 取极小值 | 单调递增 |
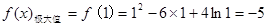 ,
,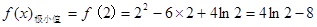 .
.函数
 的图象大致如下:
的图象大致如下: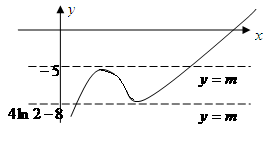
所以若函数
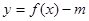 有三个不同的零点,
有三个不同的零点,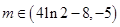 .
.(3)由题意,当
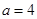 时,
时,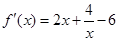 ,则在点P处切线的斜率
,则在点P处切线的斜率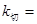
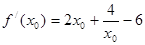 ;所以
;所以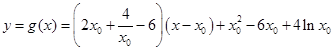
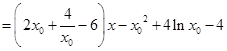 .
.令
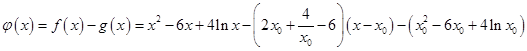 ,
,则
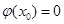 ,
,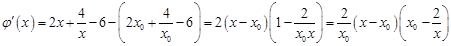 .
.当
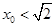 时,
时,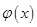 在
在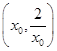 上单调递减,所以当
上单调递减,所以当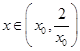 时,
时,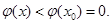 从而有
从而有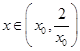 时,
时,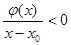 ;
;当
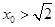 时,
时,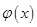 在
在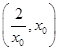 上单调递减,所以当
上单调递减,所以当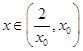 时,
时,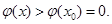 从而有
从而有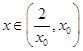 时,
时,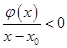 ;所以在
;所以在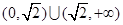 上不存在“类对称点”.
上不存在“类对称点”.当
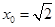 时,
时,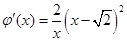 ,所以
,所以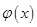 在
在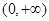 上是增函数,故
上是增函数,故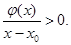
所以
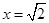 是一个类对称点的横坐标.
是一个类对称点的横坐标.点评:解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,注意导数性质的灵活运用.

练习册系列答案
相关题目
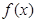 在
在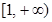 上为增函数,求正实数
上为增函数,求正实数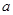 的取值范围;
的取值范围;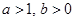 ,求证:
,求证: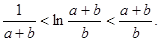
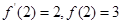 ,则
,则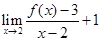 的值为 ( )
的值为 ( ) 的导函数
的导函数 ,则函数
,则函数 的单调递减区间是( )
的单调递减区间是( )



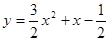 的某一切线与直线
的某一切线与直线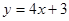 平行,则切点坐标
平行,则切点坐标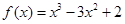 在区间
在区间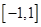 上的最大值是
上的最大值是 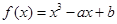 外的点A(1,0)作曲线C的切线恰有两条,
外的点A(1,0)作曲线C的切线恰有两条,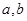 满足的等量关系;
满足的等量关系;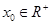 ,使
,使 成立,求
成立,求 的取值范围.
的取值范围.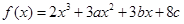 在
在 及
及 时取得极值.
时取得极值. 的值;
的值;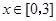 ,都有
,都有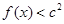 成立,求c的取值范围.
成立,求c的取值范围.