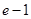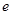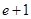题目内容
(本小题满分12分)
设函数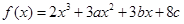 在
在 及
及 时取得极值.
时取得极值.
(I)求 的值;
的值;
(II)若对于任意的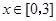 ,都有
,都有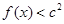 成立,求c的取值范围.
成立,求c的取值范围.
设函数
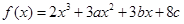 在
在 及
及 时取得极值.
时取得极值.(I)求
 的值;
的值;(II)若对于任意的
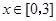 ,都有
,都有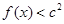 成立,求c的取值范围.
成立,求c的取值范围.(I)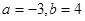 (II)
(II)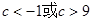
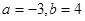 (II)
(II)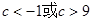
试题分析:(I)由题意知,
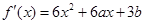 ,
,因为函数在
 及
及 时取得极值,所以
时取得极值,所以 及
及 是导函数的两个根,
是导函数的两个根,由韦达定理知:
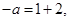
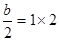 ,即
,即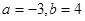 . ……6分
. ……6分(II)由(I)知
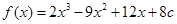 ,
,所以
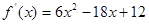 ,
,令
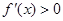 得:
得: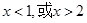 ,
,所以当
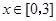 时,函数在
时,函数在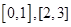 上单调递增,在
上单调递增,在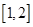 上单调递减, ……8分
上单调递减, ……8分又因为
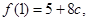
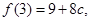 所以
所以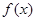 在
在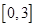 上的最大值为
上的最大值为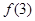 , ……10分
, ……10分所以
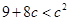 ,解得:
,解得: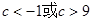 . ……12分
. ……12分点评:函数的极值点一定是导函数为零的点,但导函数为零的点不一定是极值点;根据函数的极值点和端点处的函数值进行比较,就能得出函数的最值,而恒成立问题一般转化为最值问题进行解决.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
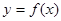 的大致图象如图所示, 则函数
的大致图象如图所示, 则函数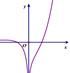
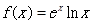
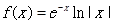
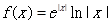
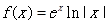
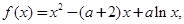 其中常数
其中常数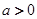 .
.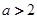 时,求函数
时,求函数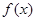 的单调递增区间;
的单调递增区间;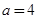 时,若函数
时,若函数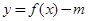 有三个不同的零点,求m的取值范围;
有三个不同的零点,求m的取值范围;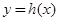 在点
在点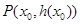 处的切线方程为
处的切线方程为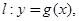 当
当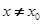 时,若
时,若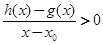 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数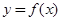 是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由. y=x(x+2)所围成的封闭图形的面积等于
y=x(x+2)所围成的封闭图形的面积等于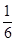
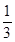
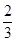
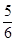
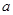 为实数,
为实数,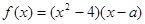 ,
,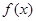 的单调递增区间;
的单调递增区间;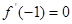 ,求
,求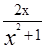 - 2的极值.
- 2的极值.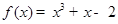 在
在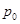 处的切线平行于直线
处的切线平行于直线 ,则
,则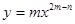 的导数为
的导数为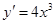 ,则( )
,则( )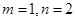
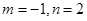
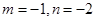
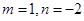
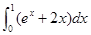 等于( )
等于( )