题目内容
若函数y=logax(a>1)的定义域和值域均为[m,n],则a的范围是 .
考点:函数的值域,函数的定义域及其求法,利用导数研究函数的极值
专题:计算题,函数的性质及应用,导数的概念及应用
分析:由题意知函数y=logax(a>1)与y=x的图象有两个不同的交点,从而转化为logax-x=0有两个不同的根,设f(x)=logax-x,利用导数求解.
解答:
解:∵函数y=logax(a>1)的定义域和值域均为[m,n],
∴函数y=logax(a>1)与y=x的图象有两个不同的交点,
即logax-x=0有两个不同的根,
设f(x)=logax-x,
则f′(x)=
-1,
令f′(x)=
-1=0得,
x=logae,
故当x=logae时,g(x)取得最大值loga(logae)-logae;
则loga(logae)-logae>0;
故1<a<e
;
故答案为:(1,e
).
∴函数y=logax(a>1)与y=x的图象有两个不同的交点,
即logax-x=0有两个不同的根,
设f(x)=logax-x,
则f′(x)=
| 1 |
| xlna |
令f′(x)=
| 1 |
| xlna |
x=logae,
故当x=logae时,g(x)取得最大值loga(logae)-logae;
则loga(logae)-logae>0;
故1<a<e
| 1 |
| e |
故答案为:(1,e
| 1 |
| e |
点评:本题考查了导数的综合应用及函数的性质与函数的图象的关系应用,属于中档题.

练习册系列答案
相关题目
函数y=x2+bx+c在区间[0,+∞)上具有单调性,则实数b应满足的条件是( )
| A、b≥0 | B、b≤0 |
| C、b>0 | D、b<0 |
已知向量
、
满足|
|=
,|
-
|=
,(
,
)=
,则|
|等于( )
| a |
| b |
| a |
| 2 |
| a |
| b |
| 5 |
| a |
| b |
| π |
| 4 |
| b |
| A、2 | ||
B、
| ||
| C、3 | ||
D、2
|
为测量地面上B,C两点间的距离,在高100m的建筑物顶部选点A,在A出测得点B,C的俯角分别为30°和45°(B,C与建筑物底部在同一水平面上),且∠BAC=45°,则B,C之间的距离为( )
| A、100m | ||
B、100
| ||
C、100
| ||
| D、200m |
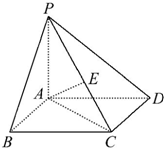 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥AB,PA⊥AC,E是PC的中点,已知AB=2,AD=PA=2,求异面直线BC与AE所成的角的大小.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥AB,PA⊥AC,E是PC的中点,已知AB=2,AD=PA=2,求异面直线BC与AE所成的角的大小.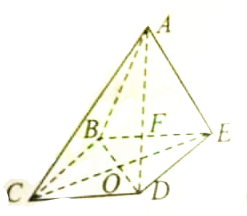 如图所示,几何体A-BCDE是底面边长为4的菱形,∠CBE=120°,侧面ABE是等边三角形,BD∩CE=O,F是BE上的动点,面ABE⊥面BCDE;
如图所示,几何体A-BCDE是底面边长为4的菱形,∠CBE=120°,侧面ABE是等边三角形,BD∩CE=O,F是BE上的动点,面ABE⊥面BCDE;