题目内容
4.设数列{an}的前n项和为Sn,已知a1=2,a2=8,Sn+1+4Sn-1=5Sn(n≥2),Tn是数列{log2an}的前n项和Tn.(1)求数列{an}的通项公式;
(2)求Tn;
(3)求满足$(1-\frac{1}{T_2})(1-\frac{1}{T_3})…(1-\frac{1}{T_n})>\frac{1011}{2014}$的最大正整数n的值.
分析 (1)由已知条件得Sn+1-Sn=4(Sn-Sn-1),从而an+1=4an,由此推导出数列{an}是以a1=2为首项,公比为4的等比数列.从而an=2•4n-1=22n-1.
(2)由log2an=log222n-1=2n-1,能求出数列{log2an}的前n项和;
(3)令$\frac{n+1}{2n}$>$\frac{1011}{2014}$,能求出满足条件的最大正整数n的值.
解答 解:(1)∵当n≥2时,Sn+1+4Sn-1=5Sn(n≥2),
∴Sn+1-Sn=4(Sn-Sn-1),
∴an+1=4an,∵a1=2,a2=8,
∴a2=4a1,
∴数列{an}是以a1=2为首项,公比为4的等比数列.
∴an=2•4n-1=22n-1.
(2)由(1)得:log2an=log222n-1=2n-1,
∴Tn=log2a1+log2a2+…+log2an
=1+3+…+(2n-1)
=$\frac{n(1+2n-1)}{2}$=n2.
(3)(1-$\frac{1}{{T}_{2}}$)(1-$\frac{1}{{T}_{3}}$)…(1-$\frac{1}{{T}_{n}}$)
=(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)…(1-$\frac{1}{{n}^{2}}$)
=$\frac{{2}^{2}-1}{{2}^{2}}$•$\frac{{3}^{2}-1}{{3}^{2}}$•$\frac{{4}^{2}-1}{{4}^{2}}$…$\frac{{n}^{2}-1}{{n}^{2}}$
=$\frac{n+1}{2n}$,
令$\frac{n+1}{2n}$>$\frac{1011}{2014}$,解得:n<251$\frac{3}{4}$,
故满足条件的最大正整数n的值是251.
点评 本题考查数列的通项公式的求法,考查数列的前n项和的求法,考查最大的正整数的求法,解题时要认真审题,注意构造法的合理运用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 30 | B. | -11 | C. | 3 | D. | 20 |
| A. | 将图象上的每一点横坐标缩短到原来的$\frac{1}{2}$而纵坐标不变 | |
| B. | 沿x向左平移$\frac{π}{2}$个单位,再把得图象上的每一点横坐标伸长到原来的2而纵坐标不变 | |
| C. | 先把图象上的每一点横坐标缩短到原来的$\frac{1}{2}$而纵坐标不变,再将所得图象沿x向右平移$\frac{π}{4}$个单位 | |
| D. | 先把图象上的每一点横坐标缩短到原来的$\frac{1}{2}$而纵坐标不变,再将所得图象沿x向左平移$\frac{π}{2}$个单位 |
| A. | 0.6 | B. | 0.48 | C. | 0.75 | D. | 0.56 |
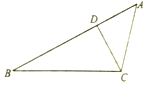 如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.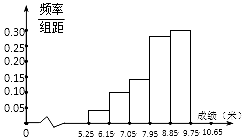 某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.