题目内容
2.圆C过点A(6,4),B(1,-1),且圆心在直线l:x-5y+7=0上.(1)求圆C的方程;
(2)P为圆C上的任意一点,定点Q(7,0),求线段PQ中点M的轨迹方程.
分析 (1)设所求圆的方程为(x-a)2+(y-b)2=r2,代入坐标,可得圆心与半径,即可求圆C的方程;
(2)利用代入法,求线段PQ中点M的轨迹方程.
解答 解:(1)设所求圆的方程为(x-a)2+(y-b)2=r2.由题意得$\left\{\begin{array}{l}{(6-a)^{2}+(0-b)^{2}={r}^{2}}\\{(1-a)^{2}+(5-b)^{2}={r}^{2}}\\{2a-7b+8=0}\end{array}\right.$----------2分
解得a=3,b=2,r=$\sqrt{13}$--------------4分
所以所求圆的方程是(x-3)2+(y-2)2=13.---------------------5分
(2)设线段PQ的中点M(x,y),P(x0,y0)
M为线段PQ的中点,则x0=2x-8,y0=2y,-----------------------------(8分)
P(2x-8,2y)代入圆C中得(2x-7-3)2+(2y-2)2=13--------------9分
即线段PQ中点M的轨迹方程为(x-5)2+(y-1)2=$\frac{13}{4}$.-----------10分.
点评 本题考查圆的方程,考查代入法的运用,确定坐标之间的关系是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
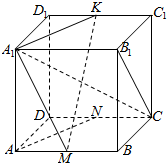 如图所示,M、N、K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.求证:
如图所示,M、N、K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.求证: