题目内容
16. 如图,在三棱锥D-ABC中,已知AB=AD=2,BC=1,$\overrightarrow{AC}•\overrightarrow{BD}=-3$,则CD=$\sqrt{7}$.
如图,在三棱锥D-ABC中,已知AB=AD=2,BC=1,$\overrightarrow{AC}•\overrightarrow{BD}=-3$,则CD=$\sqrt{7}$.
分析 用$\overrightarrow{AB},\overrightarrow{AD}$表示$\overrightarrow{BD}$,根据已知条件列方程得出AC,∠BAC,∠DAC的关系,使用等量代换计算CD2=|$\overrightarrow{AD}-\overrightarrow{AC}$|2.
解答 解:设∠BAC=α,∠DAC=β,
∵|$\overrightarrow{AC}-\overrightarrow{AB}$|=BC=1,
∴AC2+AB2-2AC•ABcosα=1,即AC2-4ACcosα=-3.
∵$\overrightarrow{AC}•\overrightarrow{BD}=-3$,
∴$\overrightarrow{AC}•(\overrightarrow{AD}-\overrightarrow{AB})$=$\overrightarrow{AC}•\overrightarrow{AD}-\overrightarrow{AC}•\overrightarrow{AB}=-3$,
即2ACcosβ-2ACcosα=-3,∴2ACcosβ=2ACcosα-3.
∴CD2=($\overrightarrow{AD}-\overrightarrow{AC}$)2=${\overrightarrow{AD}}^{2}$+${\overrightarrow{AC}}^{2}$-2$\overrightarrow{AC}•\overrightarrow{AD}$=4+AC2-4ACcosβ=4+AC2-4ACcosα+6=7.
∴CD=$\sqrt{7}$.
故答案为$\sqrt{7}$.
点评 本题考查了空间向量的数量积运算,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
4.复数z满足z(1+$\sqrt{3}\\;i$i)=|1+$\sqrt{3}$i|,则z等于( )
| A. | 1-$\sqrt{3}$i | B. | 1 | C. | $\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i | D. | $\frac{\sqrt{3}}{2}$-$\frac{1}{2}$i |
11.已知向量$\overrightarrow{m}$=(1,cosθ),$\overrightarrow{n}$=(sinθ,-2),且$\overrightarrow{m}$⊥$\overrightarrow{n}$,则sin2θ+6cos2θ的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | -2 |
1.已知向量$\overrightarrow a=(cosθ,-sinθ),\overrightarrow b=(-cos2θ,sin2θ)(θ∈(π,2π))$,若向量$\overrightarrow a,\overrightarrow b$的夹角为φ,则有( )
| A. | φ=θ | B. | φ=π-θ | C. | φ=θ-π | D. | φ=θ-2π |
8.若tanα=$\frac{1}{3}$,则cos($\frac{π}{2}$+2α)=( )
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
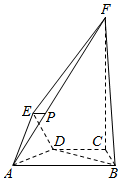 如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.
如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.