题目内容
6.设f(x)是二次函数,其图象过点(0,1),且在点(-2,f(-2))处的切线方程为2x+y+3=0.(1)求函数f(x)的表达式
(2)求函数f(x)的图象与两坐标轴所围成的图形的面积;
(3)若直线x=-t(0<t<1)把f(x)的图象与两坐标轴所围成的图形的面积二等分,求t的值.
分析 (1)根据导函数的解析式设出原函数的解析式,根据有两个相等的实根可得答案.
(2)根据定积分的定义可得答案.
(3)由题意可得${∫}_{-1}^{-t}$(x2+2x+1)dx=${∫}_{-t}^{0}$(x2+2x+1)dx,化简得2(t-1)3=-1,由此求得t的值.
解答 解:(1)设f(x)=ax2+bx+c,f′(x)=2ax+b,
∴$\left\{\begin{array}{l}{f(0)=c=1}\\{f(-2)=4a-2b+c=1}\\{f′(-2)=-4a+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=2}\\{c=1}\end{array}\right.$,
∴f(x)=x2+2x+1;
(2)S=${∫}_{-1}^{0}$(x2+2x+1)dx=($\frac{1}{3}$x3+x2+x) ${|}_{-1}^{0}$=$\frac{1}{3}$.
(3)由题意可得${∫}_{-1}^{-t}$(x2+2x+1)dx=${∫}_{-t}^{0}$(x2+2x+1)dx
即 ($\frac{1}{3}$x3+x2+x)${|}_{-1}^{0}$=($\frac{1}{3}$x3+x2+x)${|}_{-1}^{0}$.
即-$\frac{1}{3}$t3+t2-t+$\frac{1}{3}$=$\frac{1}{3}$t3-t2+t,∴2t3-6t2+6t-1=0,
即2(t-1)3=-1,∴t=1-$\frac{1}{\root{3}{2}}$.
点评 本题主要考查用待定系数法求函数的解析式,导数的运算,定积分的应用,属于中档题.

练习册系列答案
相关题目
 如图,在三棱锥D-ABC中,已知AB=AD=2,BC=1,$\overrightarrow{AC}•\overrightarrow{BD}=-3$,则CD=$\sqrt{7}$.
如图,在三棱锥D-ABC中,已知AB=AD=2,BC=1,$\overrightarrow{AC}•\overrightarrow{BD}=-3$,则CD=$\sqrt{7}$.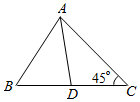 如图,在△ABC中,点D在边BC上,BD=2,BA=3,AD=$\sqrt{7}$,∠C=45°.
如图,在△ABC中,点D在边BC上,BD=2,BA=3,AD=$\sqrt{7}$,∠C=45°. 如图所示,在平面直角坐标系xOy中,点A在x轴正半轴上,直线AB的倾斜角为$\frac{3π}{4}$,OB=4,设∠AOB=θ,θ∈($\frac{π}{2}$,$\frac{3π}{4}$).
如图所示,在平面直角坐标系xOy中,点A在x轴正半轴上,直线AB的倾斜角为$\frac{3π}{4}$,OB=4,设∠AOB=θ,θ∈($\frac{π}{2}$,$\frac{3π}{4}$).