题目内容
9.在以O为极点的极坐标系中,曲线ρ=2cosθ和直线ρcosθ=a相交于A,B两点.若△AOB是等边三角形,则a的值为$\frac{3}{2}$.分析 求出曲线的直角坐标方程为:x2+y2-2x=0,直线的直角坐标方程为:x=a,作出图形,利用勾股定理能求出a的值.
解答 解:∵曲线ρ=2cosθ和直线ρcosθ=a,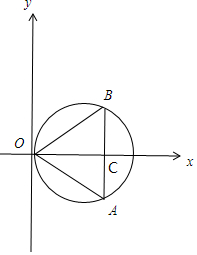
∴曲线的直角坐标方程为:x2+y2-2x=0,
直线的直角坐标方程为:x=a,
∵曲线ρ=2cosθ和直线ρcosθ=a相交于A,B两点.△AOB是等边三角形,
∴如图,设OC=a,BC=b,则$\sqrt{3}b$=a,解得b=$\frac{\sqrt{3}}{3}a$,
∴B(a,$\frac{\sqrt{3}}{3}$a),∴${a}^{2}+(\frac{\sqrt{3}}{3}a)^{2}-2×a=0$,
解得a=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意极坐标和直角坐标的互化公式的合理运用.

练习册系列答案
相关题目
19.执行如图所示的程序框图,输出的y值为( )
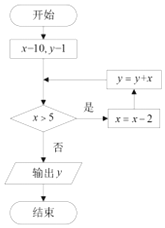

| A. | 15 | B. | 17 | C. | 19 | D. | 21 |
20.已知数列{an}是等差数列,若a2016+a2017<0,a2016•a2017<0,且数列{an}的前n项和Sn有最小值,那么Sn取得最小正值时,n等于( )
| A. | 4029 | B. | 4030 | C. | 4031 | D. | 4032 |
17.已知点P在函数$f(x)=ln({2x+1})+\frac{{{x^2}+x}}{8}$图象上,则函数f(x)在点P处切线倾斜角α的取值范围( )
| A. | $[{\frac{π}{4},\frac{π}{2}})$ | B. | $[{\frac{π}{4},\frac{3π}{4}}]$ | C. | $[{\frac{π}{4},π})$ | D. | $[{0,\frac{π}{4}}]$ |
4.已知集合A={x|x2-x-2≤0},B={x∈N+|0≤x≤3},则A∩B=( )
| A. | {0,1} | B. | {0,1,2} | C. | {0,1,2,3} | D. | ∅ |
14.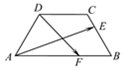 如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )
如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )
 如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )
如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )| A. | λ∈($\frac{1}{8}$,$\frac{1}{4}$) | B. | λ∈($\frac{1}{4}$,$\frac{3}{8}$) | C. | λ∈($\frac{3}{8}$,$\frac{1}{2}$) | D. | λ∈($\frac{1}{2}$,$\frac{5}{8}$) |
19.已知集合A={x|x2≤4},$B=\left\{{\left.x\right|\frac{x-1}{x-2}≤0}\right\}$,则A∩B( )
| A. | [-2,2) | B. | [1,2) | C. | (-2,1] | D. | (1,2] |