曲线y=sinx+cosx在x=$\frac{π}{4}$处切线倾斜角的大小是( )A．0B．$\frac{π}{4}$C．-$\frac{π}{4}$D．$\frac{3π}{4}$ 题目和参考答案——青夏教育精英家教网—

题目内容

4．曲线y=sinx+cosx在x=$\frac{π}{4}$处切线倾斜角的大小是（　　）

A．

B．

$\frac{π}{4}$

C．

-$\frac{π}{4}$

D．

$\frac{3π}{4}$

分析求出函数的导数，求出导数值，然后求解切线的倾斜角．

解答解：曲线y=sinx+cosx，可得y′=-sinx+cosx，
曲线y=sinx+cosx在x=$\frac{π}{4}$处切线的斜率为：0．
曲线y=sinx+cosx在x=$\frac{π}{4}$处切线倾斜角的大小是：0．
故选：A．

点评本题考查函数的导数的应用，切线的斜率以及倾斜角的求法，考查计算能力．

练习册系列答案

相关题目

14．

如图，将正三角形ABC分割成m个边长为1的小正三角形和一个灰色菱形，这个灰色菱形可以分割成n个边长为1的小正三角形．若m：n=47：25，则三角形ABC的边长是（　　）

15．

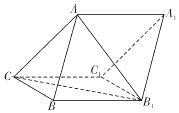如图，三棱柱ABC-A₁B₁C₁中，侧面BB₁C₁C为菱形，AC=AB₁．
（1）证明：AB⊥B₁C；
（2）若$B{B_1}=a，∠CB{B_1}=\frac{2π}{3}$，平面AB₁C⊥平面BB₁C₁C，直线AB与平面BB₁C₁C所成角为$\frac{π}{4}$，求点B₁到平面ABC的距离．

12．集合A={x|-2≤x≤3}，B={x|x＜-1}，则A∩（∁_RB）等于（　　）

19．

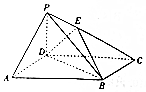如图所示，在四棱锥P-ABCD中，底面ABCD为平行四边形，∠DBA=30°，$\sqrt{3}$AB=2BD，PD=AD，PD⊥底面ABCD，E为PC上一点，且PE=$\frac{1}{2}$EC．
（1）证明：PA⊥BD；
（2）若AD=$\sqrt{6}$，求三棱锥E-CBD的体积．

9．已知等边三角形的一个顶点位于原点，另外两个顶点在抛物线y²=2$\sqrt{3}$x上，则这个等边三角形的边长为（　　）

A．

6$\sqrt{3}$

B．

$\frac{2\sqrt{3}}{3}$

C．

D．

16．在平面直角坐标系xOy中，双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-y²=1（a＞0）的左右焦点分别为F₁、F₂，离心率为$\frac{2\sqrt{3}}{3}$，且经过右焦点F₂的直线l与双曲线的右支交于A、B两点．
（1）求双曲线E的方程；
（2）求△ABF₁的面积的取值范围．

13．已知函数f（x）=xlnx+a（a∈R），g（x）=$\frac{2x}{{e}^{x-1}}$-e（e为自然对数的底数）．
（Ⅰ）讨论函数f（x）的零点个数；
（Ⅱ）求证：当x＞0时，f（x）＞g（x）+a．

5．已知集合A={x∈N₊|3x-9＜0}，集合B={x|$\frac{1}{2}$＜2^x＜8}，集合C={1，2a-4}．
（1）求A∩B；
（2）若C⊆（A∩B），求实数a的值．

试题分类