题目内容

20．已知f（x-1）=x2+4x-5，则f（x）的表达式是（　　）
A．x2+6xB．x2+8x+7C．x2+2x-3D．x2+6x-10

分析 令x-1=t，得x=t+1，将已知表达式写成关于t的表达式，再将t换回x即可得到f（x）的表达式．

解答 解：令x-1=t，得x=t+1
∵f（x-1）=x2+4x-5，
∴f（t）=（t+1）2+4（t+1）-5=t2+6t，
由此可得f（x）=x2+6x
故选：A．

点评 本题给出函数f（x-1）的表达式，求f（x）的表达式．考查了函数的定义和解析式的求法等知识，属于基础题．

练习册系列答案
相关题目
10．在区间[0，4]上任取一个实数x，则x＞1的概率是（　　）
A．0.25B．0.5C．0.6D．0.75
11．m，n是两条不同的直线，α，β是两个不同的平面，下列命题是真命题的是（　　）
A．若m∥α，m∥β，则 α∥βB．若m∥α，α∥β，则 m∥β
C．若m?α，m⊥β，则 α⊥βD．若m?α，α⊥β，则 m⊥β
8．已知M（x1，0），N（x2，$\frac{{\sqrt{2}}}{2}A}$）在函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象上，|x1-x2|的最小值$\frac{π}{3}$，则ω=（　　）
A．$\frac{3}{4}$B．$\frac{1}{3}$C．2D．1
15．已知不等式（ax+3）（x2-b）≤0对任意x∈（-∞，0）恒成立，其中a，b是整数，则a+b的取值的集合为   {4，10}   ．
5．已知定义在（-1，1）上的函数f（x）满足：对任意x，y∈（-1，1）都有f（x）+f（y）=f（x+y）．
（Ⅰ）求证：函数f（x）是奇函数；
（Ⅱ）如果当x∈（-1，0]时，有f（x）＜0，试判断f（x）在（-1，1）上的单调性，并用定义证明你的判断；
（Ⅲ）在（Ⅱ）的条件下，若a-8x+1＞0对满足不等式f（x-$\frac{1}{2}$）+f（$\frac{1}{4}$-2x）＜0的任意x恒成立，求a的取值范围．
12．y=lg|x-1|的图象为（　　）
A．B．C．D．
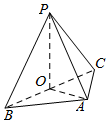9．如图，在三棱锥P-ABC中，△PAB和△PAC均为边长是$\sqrt{2}$的正三角形，且∠BAC=90°，O为BC的中点．
（Ⅰ）证明：PO⊥平面ABC；
（Ⅱ）求直线PB与平面PAC所成角的正弦值．
10．某人从甲地去乙地共走了500m，途经一条宽为x m的河流，该人不小心把一件物品丢在途中，若物品掉在河里就找不到，若物品不掉在河里就能找到．已知该物品能被找到的概率为$\frac{24}{25}$，则河宽为（　　）
A．80 mB．20 mC．40 mD．50 m

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网