题目内容
(本小题满分18分)设数列{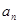 }的前
}的前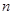 项和为
项和为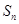 ,且满足
,且满足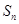 =2-
=2-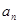 ,(
,(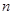 =1,2,3,…)
=1,2,3,…)
(Ⅰ)求数列{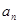 }的通项公式;
}的通项公式;
(Ⅱ)若数列{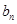 }满足
}满足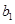 =1,且
=1,且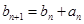 ,求数列{
,求数列{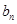 }的通项公式;
}的通项公式;
(Ⅲ)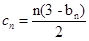 ,求
,求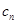 的前
的前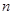 项和
项和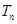
(Ⅰ) an=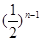 (n∈N*); (Ⅱ) bn=3-2(
(n∈N*); (Ⅱ) bn=3-2(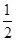 )n-; (Ⅲ)
)n-; (Ⅲ) 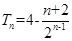 。
。
解析试题分析:(Ⅰ)∵n=1时,a1+S1=a1+a1=2
∴a1=1
∵Sn=2-an即an+Sn=2 ∴an+1+Sn+1=2
两式相减:an+1-an+Sn+1-Sn=0
即an+1-an+an+1=0,故有2an+1=an
∵an≠0 ∴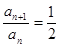 (n∈N*)
(n∈N*)
所以,数列{an}为首项a1=1,公比为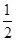 的等比数列.an=
的等比数列.an=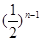 (n∈N*)
(n∈N*)
(Ⅱ)∵bn+1=bn+an(n=1,2,3,…)
∴bn+1-bn=(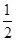 )n-1
)n-1
得b2-b1=1
b3-b2=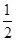
b4-b3=(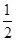 )2
)2
……
bn-bn-1=(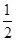 )n-2(n=2,3,…)
)n-2(n=2,3,…)
将这n-1个等式相加,得
bn-b1=1+
又∵b1=1,∴bn=3-2(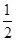 )n-1(n=1,2,3,…)
)n-1(n=1,2,3,…)
(3)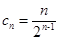
所以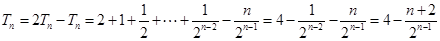
考点:数列通项公式的求法;数列前n项和的求法。
点评:若已知递推公式为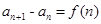 的形式求通项公式常用累加法。
的形式求通项公式常用累加法。
注:①若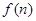 是关于n的一次函数,累加后可转化为等差数列求和;
是关于n的一次函数,累加后可转化为等差数列求和;
②若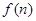 是关于n的二次函数,累加后可分组求和;
是关于n的二次函数,累加后可分组求和;
③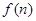 是关于n的指数函数,累加后可转化为等比数列求和;
是关于n的指数函数,累加后可转化为等比数列求和;
④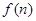 是关于n的分式函数,累加后可裂项求和。
是关于n的分式函数,累加后可裂项求和。

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
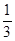 )是函数
)是函数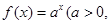 且
且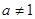 )的图象上一点,等比数列
)的图象上一点,等比数列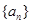 的前
的前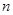 项和为
项和为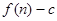 ,数列
,数列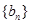
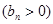 的首项为
的首项为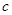 ,且前
,且前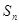 满足
满足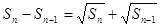 (
(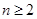 ).
).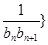 前
前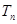 ,问
,问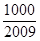 的最小正整数
的最小正整数 }是公差为正数的等差数列,数列{
}是公差为正数的等差数列,数列{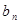 }的前n项和为
}的前n项和为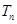 ,且
,且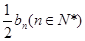
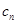 =
=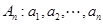 ,(例如
,(例如 时,
时,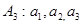 )满足
)满足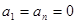 ,且当
,且当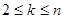 (
(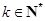 )时,
)时,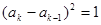 .令
.令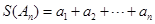 .
.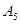 的所有可能的情况;(5分)
的所有可能的情况;(5分)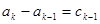 ,求
,求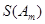 (用
(用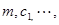
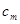 的代数式来表示);(5分)
的代数式来表示);(5分)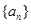 的前
的前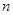 项和
项和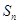 和通项
和通项 满足
满足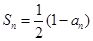 .
.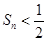 ;
;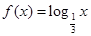 ,
,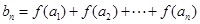 ,求
,求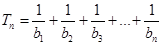 .
.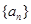 的前
的前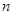 项和
项和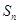 满足
满足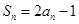 ,等差数列
,等差数列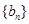 满足
满足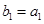 ,
,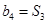 。
。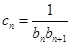 ,数列
,数列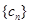 的前
的前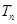 ,问
,问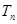 >
>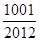 的最小正整数
的最小正整数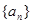 满足
满足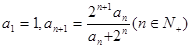
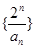 是等差数列; (2)求数列
是等差数列; (2)求数列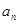 ;
; ,求数列
,求数列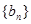 的前
的前 项和
项和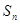 。
。 数列
数列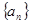 的前n项和为
的前n项和为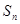 ,
, ,在曲线
,在曲线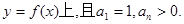
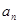 }的通项公式
}的通项公式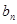 }首项b1=1,前n项和Tn,且
}首项b1=1,前n项和Tn,且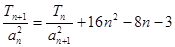 ,求数列{
,求数列{ 的首项
的首项 ,前
,前 项和为
项和为 ,满足关系
,满足关系 (
( ,
, ,3,4…)
,3,4…) ,作数列
,作数列 ,使
,使 ,
, .(
.(
 …
… 的值
的值