题目内容
(本题12分)
已知数列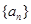 的前
的前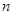 项和
项和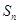 满足
满足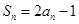 ,等差数列
,等差数列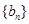 满足
满足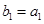 ,
,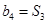 。
。
(1)求数列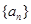 、
、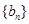 的通项公式;
的通项公式;
(2)设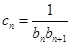 ,数列
,数列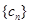 的前
的前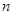 项和为
项和为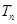 ,问
,问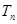 >
>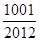 的最小正整数
的最小正整数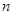 是多少?
是多少?
(1)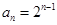 ,
,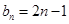 。(2)101.
。(2)101.
解析试题分析:(1)当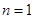 时,
时, ,∴
,∴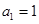 …………1分
…………1分
当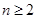 时,
时,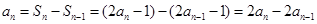 , 即
, 即 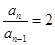
∴数列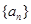 以
以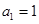 为首项,
为首项,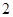 为公比的等比数列,∴
为公比的等比数列,∴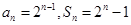 …3分
…3分
设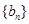 的公差为
的公差为
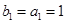 ,
,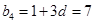 ,∴
,∴
∴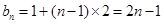 ………………………………6分
………………………………6分
(2)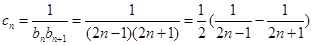 …………………………8分
…………………………8分
∴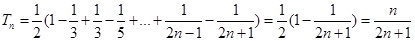 ……10分
……10分
由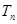 >
>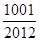 ,得
,得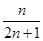 >
>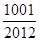 ,解得
,解得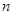 >
>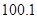 所以正整数
所以正整数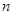 是
是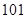 ………12分
………12分
考点:等差数列的性质;等比数列的性质;通项公式的求法;前n项和的求法。
点评:我们要熟练掌握求数列通项公式的方法。公式法是求数列通项公式的基本方法之一,常用的公式有:等差数列的通项公式、等比数列的通项公式及公式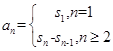 。此题的第一问求数列的通项公式就是用公式
。此题的第一问求数列的通项公式就是用公式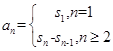 ,用此公式要注意讨论
,用此公式要注意讨论 的情况。
的情况。

练习册系列答案
相关题目
数列{an}满足4a1=1,an-1=[(-1)nan-1-2]an(n≥2),(1)试判断数列{1/an+(-1)n}是否为等比数列,并证明;(2)设an2?bn=1,求数列{bn}的前n项和Sn.
已知 若
若 在
在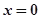 处连续,则
处连续,则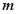 的值为( )
的值为( )
A.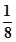 | B.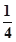 | C. | D.2 |
 的通项公式为
的通项公式为
 的值;
的值; 的值,并用数学归纳法证明你的猜想.
的值,并用数学归纳法证明你的猜想.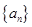 和
和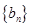 满足
满足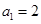 ,
,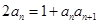 ,
,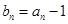 。
。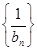 为等差数列,并求数列
为等差数列,并求数列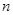 项和为
项和为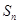 ,令
,令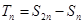 ,求
,求 的最小值。
的最小值。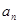 }的前
}的前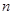 项和为
项和为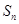 ,且满足
,且满足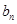 }满足
}满足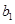 =1,且
=1,且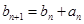 ,求数列{
,求数列{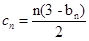 ,求
,求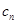 的前
的前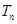
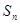 是等比数列
是等比数列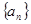 的前
的前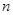 项和,且
项和,且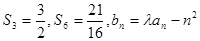 .
. ;
;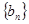 是单调递减数列,求实数
是单调递减数列,求实数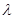 的取值范围.
的取值范围.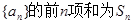 ,
,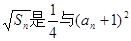 的等比中项。
的等比中项。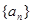 是等差数列;
是等差数列;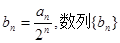 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。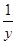 )+(x2+
)+(x2+ )+…+(xn+
)+…+(xn+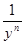 )(y
)(y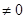 )。
)。