题目内容
定义数列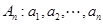 ,(例如
,(例如 时,
时,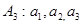 )满足
)满足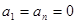 ,且当
,且当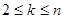 (
(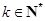 )时,
)时,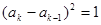 .令
.令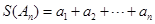 .
.
(1)写出数列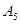 的所有可能的情况;(5分)
的所有可能的情况;(5分)
(2)设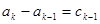 ,求
,求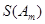 (用
(用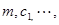
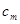 的代数式来表示);(5分)
的代数式来表示);(5分)
(3)求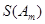 的最大值.(6分)
的最大值.(6分)
(1)由题设,满足条件的数列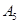 的所有可能情况有:
的所有可能情况有:
(1)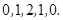 ; (2)
; (2)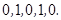 ;
;
(3)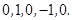 ; (4)
; (4)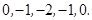 ;
;
(5)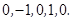 ; (6)
; (6)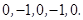 ;
;
2个起评,对2个1分,3个2分,4个3分,5个4分,6个5分
(2)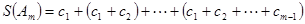
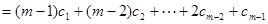 .
.
(3)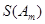 的最大值为
的最大值为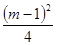 .
.
解析试题分析:(1)由题设,满足条件的数列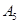 的所有可能情况有:
的所有可能情况有:
(1)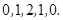 ; (2)
; (2)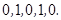 ;
;
(3)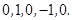 ; (4)
; (4)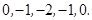 ;
;
(5)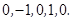 ; (6)
; (6)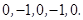 ;
;
2个起评,对2个1分,3个2分,4个3分,5个4分,6个5分
(2) ,由
,由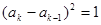 ,
,
则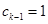 或
或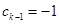 (
(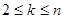 ,
,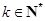 ), 6分
), 6分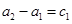 ,
,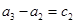 ,
,
…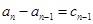 ,
,
所以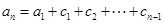 . 7分
. 7分
因为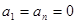 ,所以
,所以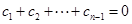 ,且
,且 为奇数, 8分
为奇数, 8分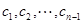 是由
是由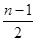 个1和
个1和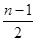 个
个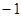 构成的数列. 9分
构成的数列. 9分
所以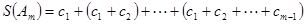
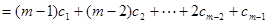 . 10分
. 10分
(3)
则当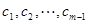 的前
的前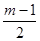 项取
项取 ,后
,后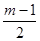 项取
项取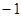 时
时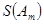 最大, 12分
最大, 12分
此时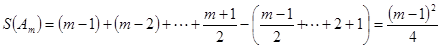 14分
14分
证明如下:
假设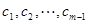 的前
的前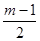 项中恰有
项中恰有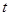 项
项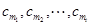 取
取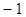 ,则
,则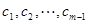 的后
的后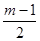 项中恰有
项中恰有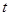 项
项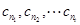 取
取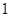 ,其中
,其中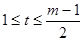 ,
,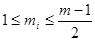 ,
,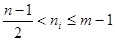 ,
,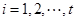 .
.
所以 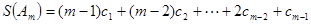 .
. 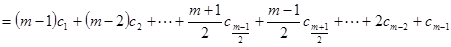
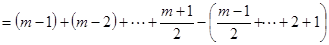
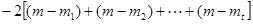
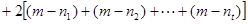
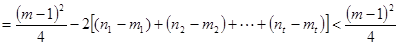 . 16分
. 16分
所以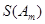 的最大值为
的最大值为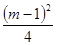 .
.
考点:本题主要考查数列的概念、通项公式,叠加法,应用不等式求最值。
点评:综合题,新定义数列问题,利用“叠加法”求得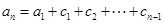 ,对考查考生灵活运用数学知识的能力起到了很好的作用。本题较难。
,对考查考生灵活运用数学知识的能力起到了很好的作用。本题较难。

练习册系列答案
相关题目
 中,
中, ,且
,且 .
.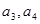 ,猜想
,猜想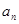 的表达式,并加以证明;
的表达式,并加以证明;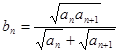 ,求证:对任意的自然数
,求证:对任意的自然数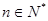 都有
都有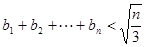 .
.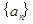 的前
的前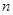 项和
项和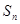 ,
,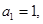
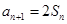 .
.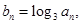 求数列
求数列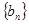 的前
的前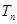 .
.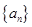 和
和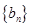 满足
满足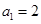 ,
,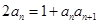 ,
,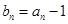 。
。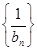 为等差数列,并求数列
为等差数列,并求数列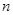 项和为
项和为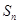 ,令
,令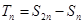 ,求
,求 的最小值。
的最小值。 是等比数列,
是等比数列,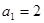 ,且
,且 是
是 的等差中项.
的等差中项.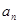 ;
;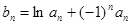 ,求数列
,求数列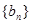 的前n项和
的前n项和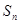 .
.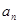 }的前
}的前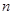 项和为
项和为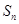 ,且满足
,且满足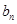 }满足
}满足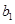 =1,且
=1,且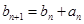 ,求数列{
,求数列{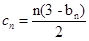 ,求
,求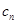 的前
的前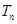
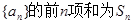 ,
,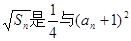 的等比中项。
的等比中项。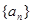 是等差数列;
是等差数列;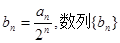 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。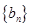 中,
中,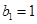 ,且点
,且点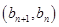 在直线
在直线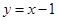 上.数列
上.数列 中,
中,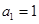 ,
, ,
, ,求数列
,求数列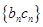 的前
的前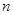 项和
项和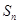 .
.