题目内容
定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是π,且当x∈[0,
]时,f(x)=sin(2x+
).
(1)求x∈[-
,0]时,f(x)的解析式;
(2)求函数f(x)的单增区间.
| π |
| 2 |
| π |
| 3 |
(1)求x∈[-
| π |
| 2 |
(2)求函数f(x)的单增区间.
考点:函数奇偶性的性质,函数的周期性
专题:三角函数的图像与性质
分析:(1)根据函数f(x)在[0,
]的解析式,结合函数的奇偶性,求出f(x)在[-
,0]上的解析式;
(2)根据函数f(x)的周期性与奇偶性,求出f(x)的单调性与单调增区间即可.
| π |
| 2 |
| π |
| 2 |
(2)根据函数f(x)的周期性与奇偶性,求出f(x)的单调性与单调增区间即可.
解答:
解:(1)当x∈[-
,0]时,-x∈[0,
],
∴f(-x)=sin(-2x+
)=-sin(2x-
);
又∵f(x)是偶函数,
∴f(x)=f(-x)=-sin(2x-
);…(6分)
(2)当x∈[0,
]时,2x+
∈[
,
],
由2x+
∈[
,
],解得x∈[0,
],
∴f(x)在[0,
]上是单调增函数,…(8分)
同理,当x∈[-
,0]时,
f(x)在x∈[-
,-
]上是单调增函数;…(10分)
由函数的周期性知,f(x)的单调递增区间是
[kπ,
+kπ]、[-
+kπ,-
+kπ],(k∈Z);…(12分)
| π |
| 2 |
| π |
| 2 |
∴f(-x)=sin(-2x+
| π |
| 3 |
| π |
| 3 |
又∵f(x)是偶函数,
∴f(x)=f(-x)=-sin(2x-
| π |
| 3 |
(2)当x∈[0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
由2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
∴f(x)在[0,
| π |
| 12 |
同理,当x∈[-
| π |
| 2 |
f(x)在x∈[-
| π |
| 2 |
| π |
| 12 |
由函数的周期性知,f(x)的单调递增区间是
[kπ,
| π |
| 12 |
| π |
| 2 |
| π |
| 12 |
点评:本题考查了三角函数的单调性与奇偶性的应用问题,也考查了利用函数的奇偶性求函数解析式的应用问题,是基础题目.

练习册系列答案
相关题目
已知
,
为不共共线的非零向量,且|
|=|
|=1,则以下四个向量中模最大者为( )
| e1 |
| e2 |
| e1 |
| e2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,PO⊥平面ABCD,点O在AB上,EA∥PO,四边形ABCD为直角梯形,且AB∥CD,BC⊥AB,BC=CD=BO=PO,EA=AO=
如图,PO⊥平面ABCD,点O在AB上,EA∥PO,四边形ABCD为直角梯形,且AB∥CD,BC⊥AB,BC=CD=BO=PO,EA=AO=
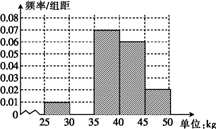 某养猪厂计划将重量为25kg到50kg的10000头猪向外出售,现从中随机抽取了100头猪进行称重,已知这些猪的重量的频率分布表及不完整的频率分布直方图(如图).
某养猪厂计划将重量为25kg到50kg的10000头猪向外出售,现从中随机抽取了100头猪进行称重,已知这些猪的重量的频率分布表及不完整的频率分布直方图(如图).