题目内容
15.设是n给定的大于2的整数,有n个外表上没有区别的袋子,第k个袋子有k个红球,n-k个白球,把这些袋子混合后,任选一个袋子,并且从中连续取出三个球(每次取出不放回),求第三次取出的是白球的概率.分析 先求出第三次取出的是白球的种数,再求出在第k个袋子中第三次取出的是白球的概率,选到第k个袋子的概率为$\frac{1}{n}$,由此能求出第三次取出的是白球的概率.
解答 解:设选出的是第k个袋,连续三次取球的方法数为n(n-1)(n-2),
第三次取出的是白球的三次取球颜色有如下四种情形:
(白白白),取法数为(n-k)(n-k-1)(n-k-2),
(白红白),取法数为k(n-k)(n-k-1),
(红白白),取法数为k(n-k)(n-k-1),
(红红白),取法数为k(k-1)(n-k),
从而第三次取出的是白球的种数为:
(n-k)(n-k-1)(n-k-2)+k(n-k)(n-k-1)+k(n-k)(n-k-1)+k(k-1)(n-k)=(n-1)(n-2)(n-k),
则在第k个袋子中第三次取出的是白球的概率pk=$\frac{n-k}{n}$,
而选到第k个袋子的概率为$\frac{1}{n}$,故所求概率为:
p=$\sum_{k=1}^{n}{p}_{k}•\frac{1}{n}$=$\sum_{k=1}^{n}\frac{n-k}{n}•\frac{1}{n}$
=$\frac{1}{{n}^{2}}\sum_{k=1}^{n}(n-k)$=$\frac{1}{{n}^{2}}\sum_{i=0}^{n-1}i$=$\frac{n-1}{2n}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
5.已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
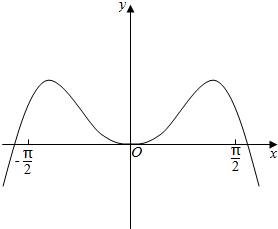

| A. | x2cosx | B. | sinx2 | C. | xsinx | D. | x2-$\frac{1}{6}$x4 |
6.数列{an}中an=$\frac{1}{{n}^{2}}$(n∈N*),f(n)=(1-a3)(1-a4)…(1-an),f(n)=( )
| A. | $\frac{2n+2}{{n}^{2}}$ | B. | $\frac{n+5}{3n}$ | C. | $\frac{2n+2}{3n}$ | D. | $\frac{2n+2}{2n+3}$ |
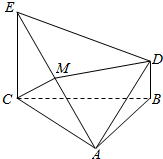 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.