题目内容
14.在平面四边形ABCD中,已知sin∠ADC=$\frac{4}{5}$,$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,|$\overrightarrow{AB}$|=1,|$\overrightarrow{AC}$|=8,求|$\overrightarrow{BD}$|的最大值4$\sqrt{2}$+5 .分析 求出△ACD的外接圆半径和圆心,根据点与圆的位置关系即可得出BD的最大值.
解答 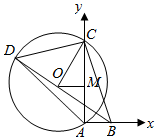 解:设△ACD的外接圆半径为r,则2r=$\frac{AC}{sin∠ADC}$=10,
解:设△ACD的外接圆半径为r,则2r=$\frac{AC}{sin∠ADC}$=10,
∴r=5.
设△ACD的外接圆圆心为O,则O到AC的距离OM=$\sqrt{{r}^{2}-(\frac{AC}{2})^{2}}$=3,
以AB,AC为坐标轴建立空间坐标系,则O(-3,4)或O(3,4),
∵D在圆O上,
∴当圆心为(-3,4),且B,O,D三点共线时,BD取得最大值.
∴|BD|的最大值为|OB|+r=$\sqrt{(-3-1)^{2}+{4}^{2}}$+5=4$\sqrt{2}$+5.
故答案为:4$\sqrt{2}$+5.
点评 本题考查了平面向量在几何中的应用,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
9.下列关于命题的说法错误的是( )
| A. | “a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件 | |
| B. | 命题“若随机变量X~N(1,4),P(X≤0)=m,则P(0<X<2)=1-2m”为真命题 | |
| C. | 命题“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” | |
| D. | 若命题P:?n∈N,2n>1000,则?P:?n∈N,2n>1000 |
10.对某产品1至6月份销售量及其价格进行调查,其售价x和销售量y之间的一组数据如表所示:
(1)根据1至5月份的数据,求解y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到
的回归方程是理想的,试问所得回归方程是否理想?
参考公式:回归直线的方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,
其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 月份i | 1 | 2 | 3 | 4 | 5 | 6 |
| 单价xi(元) | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
| 销售量yi(件) | 11 | 10 | 8 | 6 | 5 | 14 |
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到
的回归方程是理想的,试问所得回归方程是否理想?
参考公式:回归直线的方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,
其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
 如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.
如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4. 当前襄阳市正在积极创建文明城市,市某交警支队为调查市民文明驾车的情况,在市区某路口随机检测了40辆车的车速.现将所得数据分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),并绘得如图所示的频率分布直方图.
当前襄阳市正在积极创建文明城市,市某交警支队为调查市民文明驾车的情况,在市区某路口随机检测了40辆车的车速.现将所得数据分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),并绘得如图所示的频率分布直方图.