题目内容
2．正三棱锥的底面边长为a，高为$\frac{\sqrt{6}}{3}$a，则求此棱锥的侧面积．分析 利用棱锥的高，侧面三角形的高，底面中心到底边的高组成直角三角形的特点计算侧面的高，从而求出侧面积．
解答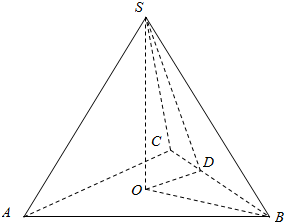 
解：设底面中心为O，过O作BC的垂线，垂足为D，连接BO，SO，SD，如图：
∵△ABC是正三角形，
∴BD=$\frac{a}{2}$，∠OBD=30°，
∴OD=$\frac{\sqrt{3}a}{6}$，
在Rt△SOD中，SD=$\sqrt{S{O}^{2}+O{D}^{2}}$=$\frac{\sqrt{3}a}{2}$．
∴S△SBC=$\frac{1}{2}×BC×SD$=$\frac{\sqrt{3}{a}^{2}}{4}$．
∴S侧面=3S△SBC=$\frac{3\sqrt{3}{a}^{2}}{4}$．
点评 本题考查了棱锥的侧面积计算，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
三棱锥O-ABC中，OA⊥OB，OB⊥OC，OC⊥OA，若OA=OB=a，OC=b，D是该三棱锥外部（不含表面）的一点，则下列命题正确的是（ ）
7．已知F1，F2分别为双曲线的左、右焦点，P为双曲线右支上的任意一点，若$\frac{|P{F}_{1}{|}^{2}}{|P{F}_{2}|}$的最小值为8a，则双曲线的离心率e的取值范围是（ ）
| A． | （1，+∞） | B． | （1，2] | C． | （1，$\sqrt{3}$] | D． | （1，3] |