题目内容
如图,椭圆C: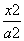 +
+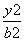 =1(a>b>0)经过点P
=1(a>b>0)经过点P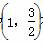 ,离心率e=
,离心率e=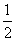 ,直线l的方程为x=4.
,直线l的方程为x=4.
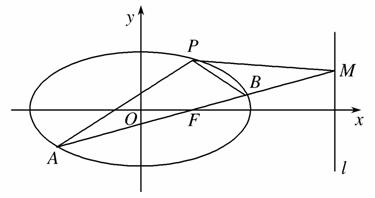
(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由.
解:(1)由P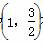 在椭圆上得,
在椭圆上得, +
+ =1①
=1①
依题设知a=2c,则b2=3c2②
②代入①解得c2=1,a2=4,b2=3.
故椭圆C的方程为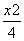 +
+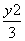 =1.
=1.
(2)由题意可设直线AB的斜率为k,
则直线AB的方程为y=k(x-1)③
代入椭圆方程3x2+4y2=12并整理,
得(4k2+3)x2-8k2x+4(k2-3)=0.
设A(x1,y1),B(x2,y2),则有
 在方程③中令x=4得,M的坐标为(4,3k).
在方程③中令x=4得,M的坐标为(4,3k).
从而k1=
由于A,F,B三点共线,则有k=kAF=kBF,即有
 ④代入⑤得k1+k2=2k-
④代入⑤得k1+k2=2k-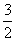 ·
·
=2k-1,
又k3=k-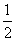 ,所以k1+k2=2k3.故存在常数λ=2符合题意.
,所以k1+k2=2k3.故存在常数λ=2符合题意.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
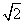 时,求直线l的方程.
时,求直线l的方程.
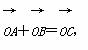 ,OC与AB交于点M.
,OC与AB交于点M.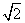 B.
B.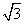 C.
C.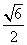
 等于( )
等于( ) 等于( )
等于( )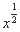 ,②y=
,②y=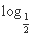 (x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )