题目内容
9.已知△ABC中,AC=4,BC=2$\sqrt{7}$,∠BAC=60°,AD⊥BC于D,则$\frac{BD}{CD}$的值为6.分析 设AB=x,由余弦定理可得:$(2\sqrt{7})^{2}$=x2+42-2x×4ccos60°,解得x=6.设BD=m,CD=n.由于AD⊥BC于D,可得$\sqrt{{6}^{2}-{m}^{2}}$=$\sqrt{{4}^{2}-{n}^{2}}$,m+n=2$\sqrt{7}$,解出即可得出.
解答 解:设AB=x,
由余弦定理可得:$(2\sqrt{7})^{2}$=x2+42-2x×4ccos60°,
化为x2-4x-12=0,
解得x=6.
设BD=m,CD=n.
∵AD⊥BC于D,
∴$\sqrt{{6}^{2}-{m}^{2}}$=$\sqrt{{4}^{2}-{n}^{2}}$,m+n=2$\sqrt{7}$,
解得m=$\frac{12\sqrt{7}}{7}$,n=$\frac{2\sqrt{7}}{7}$,
∴$\frac{DB}{CD}$=$\frac{m}{n}$=6.
故答案为:6.
点评 本题考查了余弦定理、勾股定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.在△ABC中,角A,B,C的对边分别为a,b,c,若2b=a+c,且A-C=90°,则cosB=( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{3}{4}$ | C. | -$\frac{1}{4}$ | D. | $\frac{2}{3}$ |
 如图已知三棱锥P-ABC,PA⊥平面ABC,AB=AC=PA=2,∠BAC=90°,D,E分别为AB,PC的中点,BF=2FC.
如图已知三棱锥P-ABC,PA⊥平面ABC,AB=AC=PA=2,∠BAC=90°,D,E分别为AB,PC的中点,BF=2FC. 中,
中, ,
, ,平面
,平面 平面
平面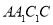 ,
,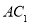 与
与 相交于点
相交于点 .
.
 ;
; 的余弦值.
的余弦值. (
( ),其中
),其中 为虚数单位,则
为虚数单位,则 ( )
( ) 的定义域是( )
的定义域是( ) B.
B. C.
C. D.
D.