题目内容
三角形两条边长分别为2和3，其夹角的余弦值是方程2
－3x＋1＝0的根，则此三角形周长为
A． | B．7 | C．5＋ | D．5＋2 |
C
解析试题分析：由已知中三角形的两边长分别为2和3，其夹角的余弦是方程2－3x＋1＝0的根，求出两边夹角的余弦，利用余弦定理可得答案．解方程2－3x＋1＝0，可知x=1,x=
,因为∵三角形的两边夹角θ的余弦是方程2－3x＋1＝0的根，因此可知
,则第三边长为
，则此三角形周长为5＋，故选C.
考点：余弦定理的运用
点评：本题考查的知识点是余弦定理的应用，其中解三角形求出两边夹角的余弦是解答的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在
中，
，则
（ ）
A． | B． | C． | D． |
在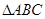
中，若
，则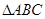是 （ ）．
| A．等边三角形 | B．等腰三角形 | C．直角三角形 | D．等腰直角三角形 |
在△ABC中，若
，则其面积等于（ ）
A． | B． | C． | D． |
在△ABC中，若a = 2 ,
,
, 则B等于 （ ）
A． | B．或  | C． | D．或 |
的左右焦点，顶点P在双曲线C上，则
得值等于（ ）
(B) 
(C) 
(D) 
若△ABC的周长等于20，面积是
，A＝60°，则BC边的长是（ ）
| A．5 | B．6 | C．7 | D．8 |
中，
,
,则
A． | B． | C． | D． |
在
中，
,则
的长为( )
A． | B．7 | C． | D．3 |