题目内容
在 中,
中, ,则
,则 的长为( )
的长为( )
A. | B.7 | C. | D.3 |
C
解析试题分析:因为由正弦面积公式可知,
再结合余弦定理得到
故选C.
考点:本题主要考查解三角形的运用。
点评:解决该试题的关键是熟练运用正弦面积公式表示出面积,同时利用余弦定理得到a的值。

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
三角形两条边长分别为2和3,其夹角的余弦值是方程2 -3x+1=0的根,则此三角形周长为
-3x+1=0的根,则此三角形周长为
A. | B.7 | C.5+ | D.5+2 |
在 中,
中, ,面积
,面积 ,则
,则 等于
等于
| A.13 | B. | C. 7 | D. |
已知 中,
中,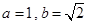 ,
, ,则角
,则角 等于( )
等于( )
A. | B. | C. | D. |
在 中
中 则
则 的值为( )
的值为( )
A. | B. | C. | D. |
在△ 中,若
中,若 ,则△
,则△ 的形状是
的形状是
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.不能确定 |
已知锐角 的面积为
的面积为 ,
, ,则角
,则角 的大小为
的大小为
| A.75° | B.60° | C.45° | D.30° |
在△ABC中,若A=60°,a=2 ,则
,则 等于 ( )
等于 ( )
| A.1 | B.2 | C.4 | D.4 |
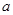 、b、c。若
、b、c。若 ,则
,则

