题目内容
若△ABC的周长等于20,面积是 ,A=60°,则BC边的长是( )
,A=60°,则BC边的长是( )
| A.5 | B.6 | C.7 | D.8 |
C
解析试题分析:依题意及面积公式S= bcsinA,得10
bcsinA,得10 =
= bcsin60°,得bc=40.又周长为20,故a+b+c=20,b+c=20-a,由余弦定理得:
bcsin60°,得bc=40.又周长为20,故a+b+c=20,b+c=20-a,由余弦定理得: =
= =
= =(b+c)2-3bc,故a2=(20-a)2-120,解得a=7.故选C
=(b+c)2-3bc,故a2=(20-a)2-120,解得a=7.故选C
考点:余弦定理
点评:考查学生利用余弦定理解决数学问题的能力,以及会用三角形的面积公式,掌握整体代换的数学思想.

练习册系列答案
相关题目
边长为 的三角形的最大角与最小角的和是( )
的三角形的最大角与最小角的和是( )
A.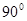 | B.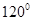 | C.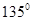 | D.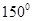 |
在 中,角
中,角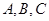 所对的边分
所对的边分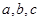 .若
.若 ,则
,则 ( )
( )
A.-  | B. | C.-1 | D.1 |
三角形两条边长分别为2和3,其夹角的余弦值是方程2 -3x+1=0的根,则此三角形周长为
-3x+1=0的根,则此三角形周长为
A. | B.7 | C.5+ | D.5+2 |
已知△ABC中,AB=6,∠A=30°,∠B=120°,则△ABC的面积( )
| A.9 | B.9 | C.18 | D. |
如图,在地面 处测得树梢的仰角为60°,
处测得树梢的仰角为60°, 与树底部
与树底部 相距为5米,则树高为( )
相距为5米,则树高为( )
A. 米 米 | B.5米 | C.10米 | D. 米 米 |
若对 恒成立,则三角形ABC是( )
恒成立,则三角形ABC是( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.不能确定形状的三角形 |
在 中,
中, ,面积
,面积 ,则
,则 等于
等于
| A.13 | B. | C. 7 | D. |
在△ 中,若
中,若 ,则△
,则△ 的形状是
的形状是
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.不能确定 |