题目内容
10.椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上任意一点M到两个焦点的距离和是4,椭圆的焦距是2,则椭圆C的标准方程是$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.分析 根据题意,由椭圆的标准方程分析可得椭圆的焦点在x轴上,再结合椭圆的定义可得2a=4,2c=2,即可得a、c的值,计算可得b的值,将a、b的值代入椭圆方程可得答案.
解答 解:根据题意,椭圆C的方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其焦点在x轴上,
又由其上任意一点M到两个焦点的距离和是4,椭圆的焦距是2,
则有2a=4,2c=2;
即a=2,c=1,
则有b2=a2-c2=3;
则椭圆的方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
故答案为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.
点评 本题考查椭圆的几何性质,关键是掌握椭圆的定义.

练习册系列答案
相关题目
2.已知长方体切去一个角的几何体直观图如图1所示给出下列4个平面图如图2:
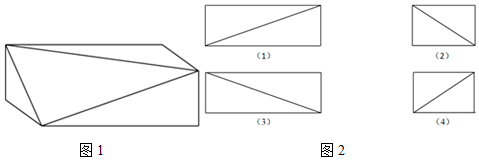
则该几何体的主视图、俯视图、左视图的序号依次是( )

则该几何体的主视图、俯视图、左视图的序号依次是( )
| A. | (1)(3)(4) | B. | (2)(4)(3) | C. | (1)(3)(2) | D. | (2)(4)(1) |
19.已知集合A={0,1,2},B={x|1≤x≤4},集合A∩B=( )
| A. | ∅ | B. | {1,2} | C. | [1,2] | D. | (1,2) |
10.已知函数f(x)=xlnx+x(x-a)2(a∈R),若存在$x∈[{\frac{1}{2},2}]$,使得f(x)>xf'(x)成立,则实数a的取值范围是( )
| A. | $({\frac{9}{4},+∞})$ | B. | $({\frac{3}{2},+∞})$ | C. | $({\sqrt{2},+∞})$ | D. | (3,+∞) |
 如图,在四棱锥P-ABCD中,$BA\user1{∥}$平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形,$PA=PD=\frac{{\sqrt{2}}}{2}CD=\sqrt{2}$.
如图,在四棱锥P-ABCD中,$BA\user1{∥}$平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形,$PA=PD=\frac{{\sqrt{2}}}{2}CD=\sqrt{2}$.