题目内容
18.已知x,y满足$\left\{\begin{array}{l}x≥0\\ y≤x\\ x+y≤k.\end{array}\right.$(k为常数),若z=x+2y最大值为8,则k=$\frac{16}{3}$.分析 由目标函数z=x+3y的最大值为8,我们可以画出满足条件的平面区域,根据目标函数的解析式形式,分析取得最优解的点的坐标,然后根据分析列出一个含参数k的方程组,消参后即可得到k的取值.
解答 解:画出满足条件的平面区域,如图示: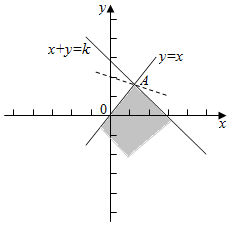 ,
,
由$\left\{\begin{array}{l}{y=x}\\{x+y=k}\end{array}\right.$,解得A($\frac{k}{2}$,$\frac{k}{2}$),
将z=x+2y转化为:y=-$\frac{1}{2}$x+$\frac{z}{2}$,
显然直线过A($\frac{k}{2}$,$\frac{k}{2}$)时,z最大,
z的最大值是:$\frac{k}{2}$+k=8,解得:k=$\frac{16}{3}$,
故答案为:$\frac{16}{3}$.
点评 如果约束条件中含有参数,我们可以先画出不含参数的几个不等式对应的平面区域,分析取得最优解是哪两条直线的交点,然后得到一个含有参数的方程(组),代入另一条直线方程,消去x,y后,即可求出参数的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知函数f(x)=Asin(ωx+φ)+m的最小值是0,最大值是4,最小正周期是$\frac{π}{2}$,其图象的一条对称轴是x=$\frac{π}{3}$,则函数f(x)的解析式应为( )
| A. | f(x)=Asin(4x+$\frac{π}{6}$) | B. | f(x)=2sin(2x+$\frac{π}{3}$)+2 | C. | f(x)=sin(4x+$\frac{π}{3}$)+2 | D. | f(x)=2sin(4x+$\frac{π}{6}$)+2 |
6.设Sn是等差数列{an}的前n项和,若a1+a2+a8+a9=20,则S9=( )
| A. | 40 | B. | 45 | C. | 50 | D. | 55 |
13.执行如图的程序框图,则输入的n=8,则输出的S=( )


| A. | $\frac{5}{14}$ | B. | $\frac{3}{8}$ | C. | $\frac{27}{56}$ | D. | $\frac{55}{56}$ |
10.若方程x2+(1-k)x-2(k+1)=0的一个根在区间(2,3)内,则实数k的取值范围是( )
| A. | (3,4) | B. | (2,3) | C. | (1,3) | D. | (1,2) |
7.已知函数f(x)=3sinωx-$\sqrt{3}$cosωx(ω>0)在区间(-ω,2ω)内单调递增,则ω的最大值为( )
| A. | $\frac{\sqrt{π}}{3}$ | B. | $\frac{\sqrt{π}}{2}$ | C. | $\frac{\sqrt{3π}}{3}$ | D. | $\frac{\sqrt{2π}}{2}$ |