题目内容
18.设a>0,函数f(x)=x+$\frac{{a}^{2}}{x}$,g(x)=x-lnx,若对任意x1∈(0,+∞),任意x2∈[1,e],都有f(x1)≥g(x2)成立,则实数a的取值范围为a≥$\sqrt{e-2}$.分析 先对函数g(x)求导判断出函数g(x)的单调性并求其最大值,然后对函数f(x)进行求导判断单调性求其最小值,最后令函数f(x)的最小值大于等于函数g(x)的最大值即可.
解答 解:∵g(x)=x-lnx,∴g'(x)=1-$\frac{1}{x}$,x∈[1,e],
g'(x)≥0,函数g(x)单调递增,
g(x)的最大值为g(e)=e-1
∵f(x)=x+$\frac{{a}^{2}}{x}$,
∴f'(x)=$\frac{{x}^{2}-{a}^{2}}{{x}^{2}}$,令f'(x)=0,∵a>0,∴x=a
当0<a<1,f(x)在[1,e]上单调增,f(1)最小=1+a2≥e-1,∴1>a≥$\sqrt{e-2}$
当1≤a≤e 列表可知 f(a)最小=2a≥e-1 恒成立
当a>e时 f(x)在[1,e]上单调减 f(e)最小=$\frac{{e}^{2}+{a}^{2}}{e}$≥e-1 恒成立
综上a≥$\sqrt{e-2}$
故答案为:a≥$\sqrt{e-2}$.
点评 本题主要考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
相关题目
8.函数f(x)的定义域为R,其导函数为f′(x).对任意的x∈R,总有f(-x)+f(x)=$\frac{{x}^{2}}{2}$,b=1;当x∈(0,+∞)时,f′(x)<$\frac{x}{2}$.若f(4-m)-f(m)≥4-2m,则实数m的取值范围是( )
| A. | [1,+∞) | B. | (-∞,1] | C. | (-∞,2] | D. | [2,+∞) |
9.设函数f(x)=$\frac{1}{3}$xlnx(x>0),则y=f(x)( )
| A. | 在区间($\frac{1}{e}$,1),(1,e)内均有零点 | |
| B. | 在区间($\frac{1}{e}$,1),(1,e)内均无零点 | |
| C. | 在区间($\frac{1}{e}$,1)内有零点,在区间(1,e内无零点 | |
| D. | 在区间($\frac{1}{e}$,1)内无零点,在区间(1,e)内有零点 |
8.已知△ABC中,a=1,B=45°,△ABC的面积为2,则三角形外接圆的半径为( )
| A. | $2\sqrt{3}$ | B. | $\frac{{5\sqrt{2}}}{2}$ | C. | $4\sqrt{2}$ | D. | $3\sqrt{2}$ |
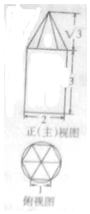 某几何体的正视图与俯视图如图所示,若俯视图中的多边形为正六边形,则该几何体的侧视图的面积为$\frac{15}{2}$.
某几何体的正视图与俯视图如图所示,若俯视图中的多边形为正六边形,则该几何体的侧视图的面积为$\frac{15}{2}$.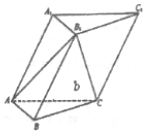 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC.