题目内容

计算：sin
25
6
π+cos
25
3
π+tan（-
25
4
π）．
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：原式利用诱导公式化简，再利用特殊角的三角函数值计算即可得到结果．
解答： 解：原式=sin（4π+
π
6
）+cos（8π+
π
3
）-tan（6π+
π
4
）=sin
π
6
+cos
π
3
-tan
π
4
=
1
2
+
1
2
-1=0．
点评：此题考查了运用诱导公式化简求值，以及特殊角的三角函数值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
相关题目
计算：（1-
1
22
）（1-
1
32
）（1-
1
42
）…（1-
1
20092
）（1-
1
20102
）
给定区域D：
x+4y≥0
x+y≤4
x+y≥2
x≥0
，令点集T={（x0，y0）∈D|x0，y0∈Z}，（x0，y）是z=x+y在D上取得最大值或最小值的点}，则T中的点最多能确定三角形的个数为（　　）
A、15B、25C、28D、32
已知函数f（x）=sin（2ωx-
π
6
）的图象关于直线x=
π
3
对称，其中ω∈（-
1
2
，
5
2
），求f（x）的解析式．
已知向量
a
=（2，0），
b
=（1，4）
（1）求2
a
+3
b
，
a
-2
b

（2）若向量k
a
+
b
与
a
+2
b
平行，求k的值．
已知函数f（x）=mlnx+
m
2
x2-x（m≠0）
（1）若函数在点（1，f（1））处的切线的斜率为1，求m的值
（2）若函数在[1，+∞）单调递增，求m的范围．
抛物线y2=12x的焦点为F，点P为抛物线上的动点，点M为其准线上的动点，当△FPM为等边三角形时，则△FPM的外接圆的方程为
 
．
2013年6月在成都举行的“《财富》全球论坛”，是继北京、上海、香港后，“论坛”第四次来到中国，也是首次登陆中国内陆地区，在一场分论坛中，A、B、C三个国家共派了五名嘉宾发言，其中A、B国各派两名，C国派一名．如果要求同一国家的嘉宾不能连续出场，则不同的安排顺序有（　　）
A、96种B、48种
C、40种D、32种
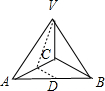在三棱锥V-ABC中，D、E分别为AB，AC的中点，平面VCB⊥平面ABC，AC⊥BC．
（1）求证：BC∥平面VDE；
（2）求证：AC⊥VB．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网