Question

已知四棱锥P-GBCD中（如图），PG⊥平面GBCD，GD∥BC，GD=

3

4

BC，且BG⊥GC，GB=GC=2，E是BC的中点，PG=4．
（Ⅰ）求异面直线GE与PC所成角的余弦值；
（Ⅱ）若F点是棱PC上一点，且

DF

•

GC

=0，

PF

=k

CF

，求k的值．

Answer 1

考点：异面直线及其所成的角,空间向量运算的坐标表示

专题：综合题,空间角

分析：（Ⅰ）在平面GBCD内，过C点作CH∥EG交GD于H，连结PH，则∠PCH（或其补角）就是异面直线GE与PC所成的角；
（Ⅱ）在平面GBCD内，过D作DM⊥GC，M为垂足，连结MF，证明FM∥PG，由

DF

•

GC

=0得GM⊥MD，故GM=GD•cos45°=

3

2

，即可得出结论．

解答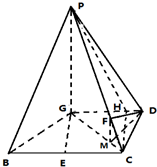： 解：（Ⅰ）在平面GBCD内，过C点作CH∥EG交GD于H，连结PH，则∠PCH（或其补角）就是异面直线GE与PC所成的角．
在△PCH中，CH=

2

，PC=

20

，PH=

18

由余弦定理得，cos∠PCH=

10

10

∴异面直线GE与PC所成角的余弦值为

10

10

．
（Ⅱ）在平面GBCD内，过D作DM⊥GC，M为垂足，连结MF，
又∵DF⊥GC，
∴GC⊥平面MFD，∴GC⊥FM
由平面PGC⊥平面ABCD，∴FM⊥平面ABCD，∴FM∥PG
由

DF

•

GC

=0得GM⊥MD，∴GM=GD•cos45°=

3

2

，
∵

PF

FC

=

GM

MC

=

3 2

1 2

=3，∴k=-3．

点评：本题考查异面直线及其所成的角，考查线面、面面垂直，考查学生分析解决问题的能力，属于中档题．