题目内容
已知椭圆E: 的左、右顶点分别为A、B,圆x2+y2=4上有一动点P,P在x轴上方,C(1,0),直线PA交椭圆E于点D,连结DC、PB.
的左、右顶点分别为A、B,圆x2+y2=4上有一动点P,P在x轴上方,C(1,0),直线PA交椭圆E于点D,连结DC、PB.
(1)若∠ADC=90°,求△ADC的面积S;
(2)设直线PB、DC的斜率存在且分别为k1、k2,若k1=λk2,求λ的取值范围.

[解析](1) 设D(x,y),∵ ∠ADC=90°,∴ .
.
即x2+y2+x-2=0.①
∵ 点D在椭圆E上,∴  .②
.②
联立①②,消去y,得3x2+4x-4=0,
∵ -2<x<2,∴ x= .
.
代入椭圆方程,得y= .
.
∴ △ADC的面积S= ×3×
×3× =
= .
.
(2)设D(x0,y0),则 ,
,
∴

 且
且
所以λ的取值范围为(-∞,0)∪(0,3).
 法二:设直线PA方程为
法二:设直线PA方程为 ,与椭圆联立方程组
,与椭圆联立方程组
 ,得
,得 ,
,
 ,
,
 ,
,

所以λ的取值范围为(-∞,0 )∪(0,3).
)∪(0,3).

练习册系列答案
相关题目
某服装加工厂某月生产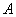 、
、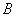 、
、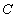 三种产品共4000件,为了保证产品质量,进行抽样检验,根据分层抽样的结果,企业统计员制作了如下的统计表格:
三种产品共4000件,为了保证产品质量,进行抽样检验,根据分层抽样的结果,企业统计员制作了如下的统计表格:
| 产品类别 |
|
|
|
| 产品数量(件) |
| ||
| 样本容量(件) | 230 |
由 于不小心,表格中
于不小心,表格中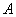 、
、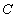 产品的有关数据已被污染看不清楚,统计员记得
产品的有关数据已被污染看不清楚,统计员记得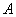 产品
产品 的样本容量
的样本容量 比
比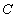 产品的样本容量多
产品的样本容量多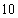 ,根据以上信息,可得
,根据以上信息,可得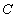 的产品数量是________.
的产品数量是________.
 2300
2300 四棱锥
四棱锥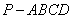 中,
中,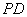 ⊥平面
⊥平面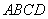 ,
,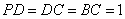 ,
,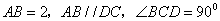 .
.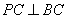 ;
; 到平面
到平面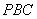 的距离.
的距离.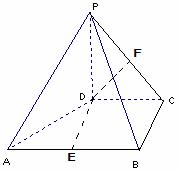
 是椭圆
是椭圆 的两个焦点,
的两个焦点, 在椭圆上,且
在椭圆上,且 ,则
,则 的面积是 .
的面积是 . ,设点F为椭圆
,设点F为椭圆 的右焦点,点M为椭圆上一动点,则
的右焦点,点M为椭圆上一动点,则 的最小值为 .
的最小值为 . 中的
中的 、
、 是函数
是函数 的极值点,则
的极值点,则 .
. 的各项均为正数,且
的各项均为正数,且 ,则
,则 .
. 的图像过点
的图像过点 ,则函数
,则函数 必过点______
必过点______ .
. ,若对任意
,若对任意 都有
都有 ,则
,则 的取值范围是 .
的取值范围是 .