题目内容
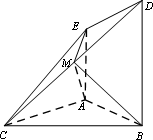
如图,四棱锥C-ABDE中,△ABC为等腰直角三角形AC=AB,AE⊥平面ABC,BD⊥平面ABC,M为
DC上一点,BD=BC=2AE=2.
(1)求证: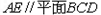
;
(2)当
时,求二面角
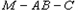的余弦值.
DC上一点,BD=BC=2AE=2.
(1)求证:
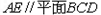; (2)当
时,求二面角的余弦值.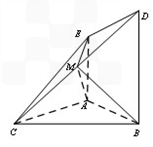
解：依题意建立如图所示空间直角坐标系, 则
,
,
,
(1)∵
∴
∴
//
而
平面
,
平面
,
∴
∥平面
(2)证明：∵
在
上,
∴
设
,则有
,
,
∴
=
∵
∴
=
解得:
,
∴
依题意
为平面
的一个法向量，
设
为平面
的一个法向量,则有
即
令
解得
,
∴
显然,二面角
为锐二面角
∴
所以,二面角
的余弦值为
,,,(1)∵
∴
∴
//而
平面,平面,∴
∥平面(2)证明：∵
在上,∴
设
,则有,,∴
=∵
∴
=解得:
,∴
依题意
为平面的一个法向量，设
为平面的一个法向量,则有即
令
解得,∴
显然,二面角
为锐二面角∴
所以,二面角
的余弦值为
练习册系列答案
相关题目
如图，四棱锥C-ABDE中，△ABC为正三角形，AE⊥平面ABC，BD⊥平面ABC，M为DC上一点，BD=BC=2AE=2．
如图，四棱锥P-ABCD中，底面ABCD 为矩形，AB=8，AD=4
（2013•南开区二模）如图，四棱锥P-ABCD的底面ABCD为菱形，∠ABC=60°，侧面PAB是边长为2的正三角形，侧面PAB⊥底面ABCD．
