题目内容
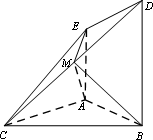
 如图,四棱锥C-ABDE中,△ABC为正三角形,AE⊥平面ABC,BD⊥平面ABC,M为DC上一点,BD=BC=2AE=2.
如图,四棱锥C-ABDE中,△ABC为正三角形,AE⊥平面ABC,BD⊥平面ABC,M为DC上一点,BD=BC=2AE=2.(Ⅰ)求证:AE∥平面BCD;
(Ⅱ)当EM⊥BD时,求二面角M-AB-C的正切值.
分析:(Ⅰ)先根据AE⊥平面ABC,BD⊥平面ABC得到AE∥BD,进而得到结论;
(Ⅱ)先在平面BCD中过点M做MN⊥BC,垂足为N,则有MN⊥平面ABC,MN∥BD;再过N做NG⊥AB于G,连接MG则MG⊥AB,可得∠MGN为二面角M-AB-C的一个平面角;最后通过求出三角形的边长即可求出结论.
(Ⅱ)先在平面BCD中过点M做MN⊥BC,垂足为N,则有MN⊥平面ABC,MN∥BD;再过N做NG⊥AB于G,连接MG则MG⊥AB,可得∠MGN为二面角M-AB-C的一个平面角;最后通过求出三角形的边长即可求出结论.
解答:解:(Ⅰ)证明:
∵AE⊥平面ABC,BD⊥平面ABC
∴AE∥BD而AE?平面BCDBD?平面BCD
∴AE∥平面BCD…(5分)
(Ⅱ)∵BD⊥平面ABC
∴平面BCD⊥平面ABC
在平面BCD中过点M做MN⊥BC,垂足为N,则有MN⊥平面ABC,MN∥BD,
∴∠EMN=
且MN∥AE
过N做NG⊥AB于G,连接MG则MG⊥AB,所以∠MGN为二面角M-AB-C的一个平面角 …(7分)
在四边形AEMN中
∵∠EAN=∠ANM=∠NME=
∴四边形AEMN为矩形
∴MN=AE=1
∴M为CD的中点,N为BC的中点 …(10分)
在Rt△MNG中,MN=1,NG=BN•sin∠ABC=
∴tan∠MGN=
=
=
…(12分)
∵AE⊥平面ABC,BD⊥平面ABC
∴AE∥BD而AE?平面BCDBD?平面BCD
∴AE∥平面BCD…(5分)
(Ⅱ)∵BD⊥平面ABC
∴平面BCD⊥平面ABC
在平面BCD中过点M做MN⊥BC,垂足为N,则有MN⊥平面ABC,MN∥BD,
∴∠EMN=
| π |
| 2 |
过N做NG⊥AB于G,连接MG则MG⊥AB,所以∠MGN为二面角M-AB-C的一个平面角 …(7分)
在四边形AEMN中
∵∠EAN=∠ANM=∠NME=
| π |
| 2 |
∴四边形AEMN为矩形
∴MN=AE=1
∴M为CD的中点,N为BC的中点 …(10分)
在Rt△MNG中,MN=1,NG=BN•sin∠ABC=
| ||
| 2 |
∴tan∠MGN=
| MN |
| NG |
| 1 | ||||
|
2
| ||
| 3 |
点评:本题主要考察直线与平面平行的判定以及二面角的平面角及求法.解决二面角的平面角问题的关键在于做出二面角的平面角.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,底面ABCD 为矩形,AB=8,AD=4
如图,四棱锥P-ABCD中,底面ABCD 为矩形,AB=8,AD=4 (2013•南开区二模)如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,侧面PAB是边长为2的正三角形,侧面PAB⊥底面ABCD.
(2013•南开区二模)如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,侧面PAB是边长为2的正三角形,侧面PAB⊥底面ABCD.