题目内容
盒中有12张花色齐全的纸牌，从中任取一张，得到红桃的概率为
，得到黑桃或方片的概率是
，得到方片或梅花的概率也是
，则任取一张，得到梅花或黑桃的概率为多少？
| 1 |
| 3 |
| 5 |
| 12 |
| 5 |
| 12 |
考点：古典概型及其概率计算公式
专题：概率与统计
分析：由题意可得红桃的张数为4，黑桃或方片共5张，方片或梅花共5张，可得方片共4张，梅花和黑桃共6张，由概率公式可得．
解答：
解：由题意可得红桃的张数为12×
=4，黑桃或方片共12×
=5张，
方片或梅花共12×
=5张，故方片共2（5+5-8）=4张，
∴梅花和黑桃共5+5-4=6张，
∴得到梅花或黑桃的概率为P=
=
| 1 |
| 3 |
| 5 |
| 12 |
方片或梅花共12×
| 5 |
| 12 |
∴梅花和黑桃共5+5-4=6张，
∴得到梅花或黑桃的概率为P=
| 6 |
| 12 |
| 1 |
| 2 |
点评：本题考查古典概型及其概率公式，属基础题．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
抛物线x2=-8y的准线方程是（ ）
A、x=
| ||
| B、y=2 | ||
C、y=
| ||
| D、y=-2 |
已知实数x，y满足
则使目标函数z=2x+y取最大值的解是（ ）
|
A、（
| ||||||||
B、（
| ||||||||
| C、（2，-2） | ||||||||
| D、（-1，1） |
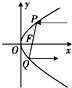为了研究探照灯的结构特征，在坐标轴中画出了探照灯的轴截面，如图．已知探照灯的轴截面图是抛物线y2=2px（p＞0）的一部分，若该抛物线的焦点恰好在直线x+y-1=0上．
如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0（