题目内容
已知tanα=3,则
= .
| sinα+cosα |
| sinα-2cosα |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:根据同角三角函数基本关系的运用化简后代入tanα=3即可求值.
解答:
解:∵tanα=3,
∴
=
=
=4.
故答案为:4.
∴
| sinα+cosα |
| sinα-2cosα |
| tanα+1 |
| tanα-2 |
| 3+1 |
| 3-2 |
故答案为:4.
点评:本题主要考查了同角三角函数基本关系的运用,属于基本知识的考查.

练习册系列答案
相关题目
已知函数y=f(x)在x=x0处可导,若
=-
,则f′(x0)等于( )
| lim |
| k→0 |
| f(x0-k)-f(x0) |
| 2k |
| 1 |
| 4 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
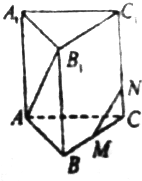 正三棱柱ABC-A1B1C1的侧棱长为2,底面边长为1,点M是BC的中点.
正三棱柱ABC-A1B1C1的侧棱长为2,底面边长为1,点M是BC的中点.