题目内容
已知曲线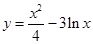 的一条切线的斜率为
的一条切线的斜率为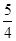 ,则切点的横坐标为( )
,则切点的横坐标为( )
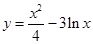 的一条切线的斜率为
的一条切线的斜率为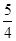 ,则切点的横坐标为( )
,则切点的横坐标为( )| A.1 | B.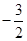 | C.4 | D.4或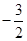 |
C
试题分析:根据斜率,对已知函数求导,解出横坐标,要注意自变量的取值区间.解:设切点的横坐标为(x0,y0),由于曲线
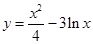 的一条切线的斜率为
的一条切线的斜率为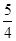 ,那么可知
,那么可知 ,那么可
,那么可 知
知 =4,故可知结论为C.
=4,故可知结论为C.点评:考查导数的几何意义,属于基础题,对于一个给定的函数来说,要考虑它的定义域.比如,该题的定义域为{x>0}.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 上,
上, 为曲线在点P处的切线的倾斜角,则
为曲线在点P处的切线的倾斜角,则 )
)


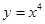 的一条切线l与直线
的一条切线l与直线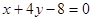 垂直,则l的方程为 ( )
垂直,则l的方程为 ( )



 的最大值为3,则
的最大值为3,则 的图象的一条对称轴的方程是 ( )
的图象的一条对称轴的方程是 ( )



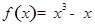 .
.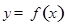 在点
在点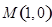 处的切线方程;
处的切线方程;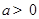 ,如果过点
,如果过点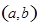 可作曲线
可作曲线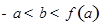
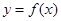 有三个零点
有三个零点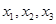 ,且在点
,且在点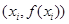 处的切线的斜率为
处的切线的斜率为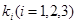 .则
.则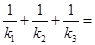 .
.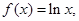 若存在函数
若存在函数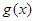 使得
使得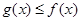 恒成立,则称
恒成立,则称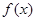 的一个“下界函数”.
的一个“下界函数”.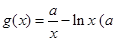 为实数
为实数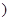 为
为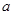 的取值范围;
的取值范围;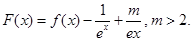 试问函数
试问函数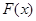 是否存在零点,若存在,求出零点个数;若不存在,请说明理由.
是否存在零点,若存在,求出零点个数;若不存在,请说明理由.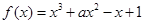 ,有下列说法:
,有下列说法: