题目内容
已知直线的极坐标方程为
，圆M的参数方程为
。求：（1）将直线的极坐标方程化为直角坐标方程；
（2）求圆M上的点到直线的距离的最小值.
（1）
；（2）
解析试题分析：（1）将
用两角和的正弦公式展开，再利用直角坐标与极坐标互化公式即可将极坐标方程化为直角坐标方程；（2）设圆上任意一点M的坐标为（
，
），利用点到直线的距离公式将点M到已知直线的距离表示为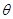
的函数，再利用三角函数求最值的方法，求出点M到直线距离的最小值,本题也可先求出圆心到直线的距离，此距离减去半径就是圆上一点到直线的距离的最小值.
试题解析：（1）方程
可化为
=1，令
，
，即得到该直线的直角坐标方程
；
（2）设圆上任意一点M的坐标为（，），则点M到该直线的距离
=
=
=
，当
时，
=
，故圆M上的点到直线的距离的最小值.
考点：极坐标方程与直角坐标方程的互化;参数方程与普通方程的互化;点线距离公式
练习册系列答案
相关题目
轴为极轴建立极坐标系，曲线
的方程为
（
为参数），曲线
的极坐标方程为
,若曲线
、
两点．
的值；
到
的参数方程为
(
为参数)，曲线
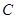的极坐标方程为
上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C.
与C的交点为
，以坐标原点为极点，x轴正半轴为极坐标建立极坐标系，求过线段
的中点且与
垂直的直线的极坐标方程.
，点P的轨迹为曲线C.
为参数，求曲线C的参数方程；
距离的最大值.
成反比，动点P的轨迹经过点(2,0)．
（
为参数），以原点为极点，x轴的正半轴为极轴，并取与直角坐标系相同的长度单位，建立极坐标系，曲线C2是极坐标方程为：
，
的最小值.